· Re-lecteur : Stéphane Ayache

· Article étudié : « Content-Faithful Transformations for MathML »

· Auteurs : Sandy Huerter, Igor Rodionov, et Stephen Watt (University of Western Ontario)

· Référence : http://www.mathmlconference.org/2002/presentations/huerter/

· Type d’article : expérience et recherche

· Notes :

	Note	Commentaire
Pertinence de l’article par rapport aux thèmes du cours	4/5	Bien que le cours mentionne seulement le standard MathML, cet article fait parfaitement ressortir l’intérêt des standards XML et XSL.
Clarté et qualité rédactionnelle	3/5	L’article est globalement clair et bien écrit. Il demande cependant une bonne connaissance préalable du standard MathML2.0. Les parties présentant les différents types de balisages parallèles sont peut être superflues, ceux ci sont parfaitement présentés dans le standard.
Globale	4/5	Le contenu de l’article est novateur dans le domaine MathML, il apporte la première transformation fidèle au contenu.

1. Pré-requis

MathML est un standard du W3C basé sur XML pour la description d’expressions mathématiques. Il permet à la fois de capturer la structure et le contenu de ces expressions. L’objectif de MathML est double : la publication de documents mathématiques sur le web, et le traitement de ces expressions par des applications de calcul formel. Dans ce sens, la DTD MathML fait la distinction entre deux types de balisages :

- Le balisage de présentation = Le "Presentation Markup" est une représentation "humaine", il n'y a aucune sémantique. Il est dédié à la publication d’expressions mathématiques.

ex : A + B = <mrow> <mi>A</mi> <mo>+</mo> <mi>B</mi> </mrow>

- Le balisage de contenu = Le "Content Markup" est dédié au calcul formel, il contient la sémantique de l'expression mathématique.

ex : la somme entre deux variables numériques A et B est définie par :

<apply>

<plus/>

</apply>

2. Résumé

Cet article s’intéresse aux transformations de documents MathML pour obtenir un balisage de présentation depuis un balisage de contenu. L’objectif de ces transformations est notamment de publier des expressions mathématiques décrites par leur contenu sémantique. Ces transformations existent depuis la première recommandation MathML du W3C ; aujourd’hui, certains navigateurs intègrent cette fonctionnalité. Ce type de transformations a l’inconvénient de perdre la sémantique du document original et empêche toute interaction entre des applications de calculs mathématiques et les navigateurs web.

La transformation présentée dans cet article offre l’avantage d’être fidèle au contenu. En effet, le document MathML résultat d’une telle transformation est défini par un balisage de présentation, tout en conservant la sémantique du document original. Par ailleurs, cette transformation est implémentée à l’aide des standards XSLT et XPath.

Une transformation fidèle au contenu nécessite l’utilisation d’un balisage parallèle, défini dans la spécification MathML2.0 du W3C. Le balisage parallèle permet de lier la présentation et le contenu de chaque expression mathématique. Il peut être de granularité haute (pour l’ensemble du document) ou fine (pour chaque partie du document).

Syntaxiquement, on définit un balisage parallèle en utilisant l'élément <semantics>, il sera père d’un arbre (ou sous-arbre) à deux branches filles : l’une ayant un balisage de contenu et l’autre un balisage de présentation ; le balisage de présentation étant généré à partir du balisage de contenu.

Une transformation fidèle au contenu à granularité fine augmente la taille du document avec un facteur de n.log(n). Ainsi, est-il préférable, dans le cas de transformations de grands documents, d’utiliser un balisage parallèle à référencement croisé, défini dans la spécification MathML2.0.

La feuille de style présentée fonctionne selon différents modes, le mode est spécifié par l’application qui l’utilise. Les deux premiers modes génèrent simplement la présentation associée au contenu, les transformations qui utilisent ces modes ne sont pas fidèles au contenu. Le deuxième mode a cependant l’avantage de conserver les correspondances sémantiques.

Les quatre modes suivant permettent une transformation fidèle au contenu, ils spécifient le type de balisage parallèle à utiliser (granularité haute, fine, référencement croisé).

Chaque mode correspond à un besoin particulier, les transformations non fidèles au contenu sont plus rapides, elles permettent par exemple un traitement en temps réel, utile pour les navigateurs web. Par ailleurs, une transformation fidèle au contenu avec granularité fine sera préférée à celle de haut niveau si l’on souhaite « copier-coller » une partie d’expression à partir d’un navigateur web vers une application de calcul mathématique…

Les éléments de contenu définis dans le standard MathML2.0 ne couvrent pas l’ensemble des concepts mathématiques. Ainsi, le standard MathML permet de définir de nouvelles balises de contenus dont la sémantique est définie par un autre langage. Il est par exemple intéressant de se référer au dictionnaire OpenMath pour sa richesse en concepts mathématiques, OpenMath étant conçu pour l’échange de données mathématiques.

L’article [1] propose des transformations entre OpenMath et MathML, celles-ci permettent notamment d’obtenir un balisage de présentation MathML pour un élément du dictionnaire OpenMath. Ceci étant, l’article étudié propose une démarche pour préserver la sémantique des éléments étendus lors d’une transformation fidèle au contenu. Les auteurs s’appuient sur une combinaisons de transformations : F est la transformation décrite dans l’article, X est une transformation qui génère la présentation associée à un élément étendu (des exemples de feuille de style d’extension sont présentés dans [8]) et A est une transformation qui modifie le préfixe (espace de nom) de l’élément étendu (A^-1 est la transformation inverse). La modification du préfixe de l’élément étendu permet de ne pas perdre la sémantique de cet élément lors de la transformation X.

La transformation fidèle au contenu d’éléments étendus est alors notée : A^-1 o X o A o F, le schéma suivant illustre une telle transformation :

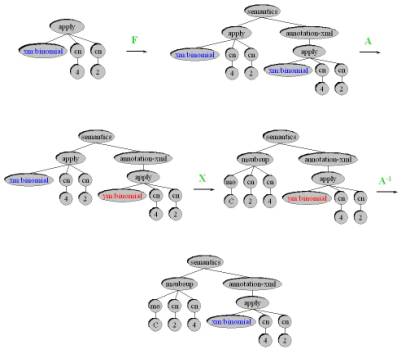
3. Commentaires

Pour ce travail de relecture, j’ai jugé pertinent de lire deux autres documents référencés par l’article étudié : la spécification MathML2.0, auquel est fortement lié cet article ; et l’article [1] qui traite des multiples transformations qu’est susceptible de subir un document mathématique.

Ces trois documents ont la caractéristique commune d’avoir été écrit conjointement par Stephen Watt.

A travers l’article étudié, nous pouvons nous rendre compte que MathML est fortement lié avec le domaine des transformations XML. C’est sans doute le standard du W3C qui dispose d’autant de possibilités de transformation.

Dans un premier temps, ce commentaire situe la transformation proposée dans l’article par rapport aux évolutions du standard MathML. La deuxième partie du commentaire présente plusieurs feuilles de styles XSL existant dans le domaine MathML. La troisième partie fera un bilan des tests réalisés pour ce travail.

3.1. Situation par rapport aux évolutions de MathML

L’article reprend une bonne partie du chapitre 5 de la spécification MathML2.0. Celle ci a fait l’objet de plusieurs modifications par rapport à MathML1.01. Le W3C a ajouté la définition d’une transformation « fidèle au contenu », ainsi que la description du balisage parallèle. On remarque ainsi que l’article est tout à fait conforme aux spécifications du W3C et qu’il exploite parfaitement les dernières évolutions du standard. En effet, le W3C définit une transformation « fidèle au contenu » comme étant une transformation qui retient le contenu original dans un balisage parallèle.

Ce lien étroit qui apparaît entre ces deux documents est d’autant plus accentué que ces derniers se référencent réciproquement… Les deux documents ont probablement été écrits durant la même période.

Cela dit, au-delà de ces similitudes, l’article étudié apporte un réel intérêt, il présente la première implémentation XSLT d’une transformation « fidèle au contenu » tel que le décrit MathML2.0. Par ailleurs, cet article propose une méthode intéressante pour conserver la sémantique des éléments étendus en s’appuyant sur les feuilles de style d’extensions présentées dans [1].

Pour des raisons d’extensibilité, MathML permet d’importer la sémantique de concepts mathématiques depuis un autre standard. Le standard OpenMath est basé sur XML pour l’échange de données mathématiques entre différentes applications. Les sémantiques des concepts qu’il manipule sont définies dans un dictionnaire qui de part sa fonction se veut exhaustif. Un auteur de documents MathML se référera, par exemple, au dictionnaire OpenMath pour utiliser des concepts qui ne sont pas définis dans la terminologie des éléments de contenu MathML.

Ainsi, la fonction de combinaison entre deux entiers (noté n’est définie que dans le dictionnaire OpenMath. Les instructions MathML suivantes permettent d’importer la définition de cette fonction depuis le dictionnaire OpenMath.

Dans un souci de simplicité et de réutilisation, le standard MathML prévoit la possibilité de remplacer les instructions précédentes par :

<xm:binomial/>

xm est l’espace de nom où est défini la balise ‘binomial’.

En balisage de contenu, s’écrirait alors :

<apply>

<xm:binomial/>

</apply>

Dans un tel cas de figure, l’article [8] décrit une transformation pour générer la présentation associée à un élément étendu. En considérant l’exemple précédent, cette transformation générerait :

</msubsup>

La méthode proposée par l’article pour préserver la sémantique des éléments étendus MathML se réfère à ce type de transformations. Ces transformations sont appelées feuilles de styles d’extensions dans la spécification MathML2.0.

Par ailleurs, la transformation présentée dans l’article requiert une légère modification pour « matcher » les éléments étendus. La version actuelle ne contient pas de « template » pour les balises non définies par la DTD MathML.

3.2. Les feuilles de styles XSL

La transformation consistant à établir une notation (balisage de présentation) à partir d’un concept mathématique (balisage de contenu) est appelée feuilles de styles de notation dans la spécification MathML2.0.

Plusieurs feuilles de style XSLT permettent de faire cette conversion, « ctop.xsl » (David Carlisle, 2001), « mathmlctop.xsl » (Emmanuel Pietriga, 2000) et sont utilisées par plusieurs projets s’appuyant sur MathML.

Si un concept est exprimable avec plusieurs notations, une règle de transformation (template) peut agir selon un paramètre de la feuille de style (ex : langue). Dans d’autres cas, on peut imaginer des transformations de documents MathML à balisage de présentation vers un autre balisage de présentation.

D’un point de vue plus général, les transformations XSLT permettent de transformer un document XML en un autre document XML. Un document MathML peut ainsi être transformé en un document XML s’appuyant sur une DTD (ou Schema XML) de nature différente.

Il existe ainsi un convertisseur MathML vers SVG (http://www.schemasoft.com/MathML) qui permet de transformer un document MathML, quel que soit son type de balisage, en un dessin vectoriel affichable par la plupart des navigateurs. SVG a l’avantage d’être largement diffusé dans l’industrie, et contrairement à MathML les nouvelles versions de navigateurs intègrent son rendu.

De nombreux outils d’éditions mathématiques proposent des fonctionnalités de conversions entre différents standards. Latex est probablement le plus connu et le plus utilisé des standards pour la publication d’expressions mathématiques. Certains environnements d’édition Latex permettent déjà d’exporter ou d’importer un document MathML. Par ailleurs, les environnements de calcul formel (Mathematica, Maple, …) intègrent ce type de conversions et s’appuient sur le balisage MathML de contenu.

3.3. Tests

J’ai souhaité tester la transformation présentée. Pour cela, j’ai utilisé le processeur XSLT Apache : XALAN. La feuille de style XSLT est en téléchargement à l’adresse : http://www.orcca.on.ca/TechReports/2000/TR-00-24.html

Le mode de la transformation est spécifié en paramètre de la feuille de style. On distingue ainsi six modes. Voici mes remarques concernant chacun des modes :

· mode = -1 : transformation non fidèle au contenu, supprime les correspondances sémantique. Il ne faut pas utiliser ce mode pour transformer des documents contenant des correspondances sémantiques.

· mode = 0 : non fidèle au contenu, conserve les correspondances sémantiques. Cette transformation est équivalentes aux feuilles de style de notations existantes.

· mode = 1 : fidèle au contenu avec balisage parallèle à granularité haute

· mode = 2 : fidèle au contenu avec balisage parallèle à granularité fine

· mode = 3 : fidèle au contenu avec référencement croisé et balisage parallèle à granularité haute. Nécessite que le balisage du document d’entrée soit préalablement parsemé d’attributs id…

· mode = 4 : fidèle au contenu avec référencement croisé. Nécessite que le balisage du document d’entrée soit préalablement parsemé d’attributs id…

4. Synthèse

L’article propose l’implémentation d’une transformation fidèle au contenu pour les documents MathML. Le standard MathML2.0 défini une transformation fidèle au contenu comme étant une transformation qui retient le contenu original dans un balisage parallèle. Les auteurs de l’article s’appuient bien sur un balisage parallèle pour conserver la sémantique originale du document. Dans ce sens, l’article est tout à fait conforme aux spécifications du W3C.

Par ailleurs, l’article va plus loin et se penche sur le cas des éléments étendus. Ces derniers n’étant pas définis dans la DTD MathML, leur transformation est plus problématique. Les auteurs suggèrent de combiner la transformation présentée avec des feuilles de styles d’extensions pour parvenir à préserver la sémantique des éléments étendus lors d’une transformation fidèle au contenu.

Le travail effectué par les auteurs de cet article prend en compte les dernières avancées effectuées dans le domaine de MathML : balisage parallèle, feuilles de styles d’extensions. La transformation présentée se situe au cœur d’une problématique avancée dans la spécification MathML2.0 : l’utilisation de MathML pour les applications interactives.

5. Références

· Spécification MathML2.0 du W3C

· [1] : Meta stylesheets for the conversion of mathematical documents in to multiple forms

(Bill Naylor, Stephen Watt, Ontario Research Centre for Computer Algebra)

Clarté et qualité rédactionnelle