La spécification du placement spatial dans Madeus telle que nous l'avons définie dans le Chapitre est un problème de maintien de solution d'un système de contraintes. L'auteur définit progressivement le placement qu'il désire obtenir en ajoutant ou retirant successivement des relations entre des éléments, ou bien en déplaçant ces derniers. Le résultat de chacune de ces actions doit prendre en compte le placement courant des éléments et les modifications apportées par cette action.
Les exemples d'applications à base de contraintes que nous avons présentés au Chapitre se situent également dans un problème de maintien de solution. La technique de résolution de contraintes utilisée dans la plupart de ces applications est une technique par propagation locale en raison, notamment, des performances obtenues.
Dans ce chapitre, nous nous proposons d'étudier plus en détail cette technique de résolution de contraintes en présentant ses avantages et ses limitations, et en montrant comment elle peut être mise en oeuvre pour maintenir le placement spatial relatif d'éléments dans Madeus.
La section 2 présente les deux approches de résolution pour le maintien de solution. La section 3 présente la technique de résolution par propagation locale. La section 4 présente les caractéristiques des résolveurs utilisant cette technique. Les sections 5 à 8 décrivent le choix de l'un de ces résolveurs dans le cadre de Madeus. La section 9 propose une synthèse sur les apports et sur les limitations de la propagation locale.
Les méthodes de résolution utilisées pour un problème de maintien de solution se divisent en deux catégories : celles qui reposent sur une approche locale et celles qui reposent sur une approche globale.
[Table des matières]
2.1 Les approches locales
Dans une approche locale, les contraintes sont traitées individuellement, de façon séquentielle. Elles n'utilisent que des informations qui leur sont disponibles immédiatement, c'est-à-dire les valeurs des variables qu'elles contraignent. Une contrainte peut être vue comme responsable d'elle même, elle a une certaine autonomie et est capable d'action et de réaction.
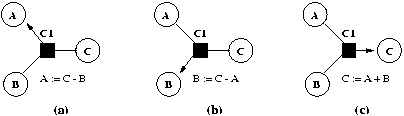
Dans un système de contraintes tel que nous l'avons défini dans la section 0.0, on associe à chaque contrainte un ensemble de méthodes de résolution qui déterminent les différentes façons de résoudre localement la contrainte. Une méthode consiste en zéro ou plusieurs variables en entrée, en une ou plusieurs variables en sortie et en une suite d'instructions qui calculent la ou les variables de sortie en fonction des variables d'entrée de manière à satisfaire la contrainte. Sur l'exemple de la contrainte C1 : C=A+B (Fig 1 ), on peut associer trois méthodes de résolution, chacune stipulant qu'une variable est calculée en fonction des deux autres: A:=C-B (Fig 1 a), B:=C-A (Fig 1 b) et C:=A+B (Fig 1 c). Si la valeur de B ou C est modifiée, alors la contrainte peut être maintenue en exécutant la première méthode.
Dans le graphe de contraintes présenté dans la section 0.0, les arêtes symbolisent l'existence de méthodes au niveau de chaque contrainte.

Fig 1. Différentes méthodes de résolution possible
L'avantage principal des approches locales réside dans leur faible coût, ce qui en fait des techniques particulièrement bien adaptées dans un contexte interactif. Leur principal inconvénient provient du fait qu'elles ne sont pas complètes, c'est-à-dire qu'elles peuvent de pas trouver de solution alors qu'il en existe.
[Table des matières]
2.2 Les approches globales
Dans une approche globale, les méthodes de résolution peuvent fournir toutes les solutions d'un système de contraintes. Pour cela, toutes les contraintes du système sont considérées, c'est-à-dire que les méthodes parcourent tous les noeuds du graphe de contraintes. De plus ces méthodes traitent généralement les contraintes de façon simultanée, comme par exemple les méthodes numériques pour résoudre un système d'équations.
L'avantage de ces approches est leur complétude car elles permettent de toujours trouver une solution si celle-ci existe. Leur inconvénient principal réside dans leur coût généralement très élevé et dans le fait qu'elles sont spécifiques à un type de données particulier (variables numériques par exemple).
Dans cette section, nous allons présenter la technique de maintien de solution par propagation locale qui est la technique utilisée dans les applications citées au chapitre précédent.
[Table des matières]
3.1 Principes de la propagation locale
Partant d'une solution perturbée, la propagation locale est une technique qui rétablit la cohérence d'un système de contraintes. Elle fonctionne en sélectionnant, puis en exécutant une séquence finie de méthodes. L'exécution d'une méthode satisfait la contrainte associée en modifiant la valeur de ses variables de sortie. Les valeurs modifiées entraînent la violation d'autres contraintes et, par propagation, l'exécution d'autres méthodes pour les satisfaire et ce, de manière récursive. L'exécution d'une méthode dont les variables de sortie ne sont reliées à aucune autre contrainte ne provoque pas de propagation .
La propagation locale se décompose en deux phases : une phase de planification et une phase d'exécution.
La phase de planification consiste à sélectionner et à ordonnancer une liste de méthodes (ou plan) pour recalculer les contraintes concernées par la perturbation initiale. Elle a pour résultat d'orienter une partie du graphe de contraintes. Ce graphe orienté est appelé graphe de solutions.
La phase d'exécution applique en séquence le plan précédemment créé.
La technique de propagation locale présente plusieurs avantages.
En premier lieu, c'est une technique très performante du fait de la séparation des phases de planification et d'exécution. En effet, la première phase, la plus coûteuse en temps n'est exécutée que lors d'une nouvelle perturbation du système. Le plan constitué pour répondre à cette perturbation peut être ensuite utilisé de façon répétitive pour répondre à la même perturbation. Ceci est très efficace dans le cadre d'interfaces graphiques où l'utilisateur veut déplacer un objet à la souris. Lorsqu'il sélectionne l'objet à déplacer, il crée une contrainte d'égalité entre la position courante de la souris et l'objet. Un plan est constitué avec les méthodes utilisées pour déplacer les objets reliés directement ou indirectement avec l'objet sélectionné. Ce plan est ensuite exécuté à chaque mouvement de la souris sur le même objet, ce qui a pour effet de modifier de façon continue la position de tous les objets concernés.
Un autre avantage de la propagation locale est qu'elle est relativement "intuitive" et simple à utiliser.
Enfin, c'est une technique générale dans le sens où elle permet de manipuler des variables de types différents (numériques, chaînes de caractères, couleurs, etc.) et de définir des méthodes de natures diverses (fonctions linéaires, quadratiques, etc.).
En contrepartie, cette technique, du fait de son approche locale possède plusieurs inconvénients. Le principal est qu'elle ne peut résoudre des contraintes qui forment des cycles. En effet, les contraintes sont traitées séparément en considérant uniquement les valeurs possibles au niveau de la contrainte, et non de manière simultanée. Les graphes de solutions qui contiennent des cycles ne peuvent pas être parcourus avec cette technique, à moins que l'utilisateur ne fournisse des informations supplémentaires.
L'autre restriction importante due à cette technique de résolution concerne le fait qu'elle ne traite que les contraintes fonctionnelles. Une contrainte est dite fonctionnelle si chacune de ses variables possède une valeur unique en fonction de la valeur des autres variables de la contrainte. Par exemple, la contrainte A <= B n'est pas une contrainte fonctionnelle car, étant donnée la valeur de B, on ne peut déterminer de façon unique la valeur de A.
Malgré ces inconvénients, la propagation locale est la technique la plus largement utilisée dans les interfaces graphiques à base de contraintes du fait de sa facilité de mise en oeuvre et de ses performances.
[Table des matières]
3.2 Propagation locale par valeurs
Différentes méthodes de propagation locale existent, la différence étant due à la façon de constituer le plan. La méthode la plus communément employée est la propagation locale par valeurs, également appelée propagation locale d'états connus.
Le principe de cette méthode est de construire le plan en partant de la perturbation initiale et en sélectionnant une méthode dès que la valeur de ses variables d'entrée est connue. L'application de cette méthode modifie ses variables de sortie qui vont être les nouvelles valeurs pour les variables d'entrée d'autres méthodes. Ce mécanisme s'interrompt lorsqu'il n'y a plus de contraintes à vérifier, c'est à dire plus de méthodes à calculer.
Dans la phase de planification, une méthode ne peut être sélectionnée que si toutes ses variables d'entrée sont renseignées et s'il n'existe pas d'autre méthode ayant déjà déterminé une de ses variables de sortie. Ceci permet d'éviter des situations de conflit où une variable se retrouverait en sortie de plusieurs méthodes.
Les méthodes sont ensuite ordonnancées de manière à pouvoir calculer une nouvelle solution en fonction de la solution initiale et de la perturbation. L'ordonnancement correspond à un tri topologique sur la partie du graphe de contraintes concernée par la perturbation.
Sur l'exemple de la Fig 2 , on considère trois contraintes C1, C2 et C3 pour lesquelles chacune des variables peut être calculée en fonction des autres variables de la contrainte. Une modification de la variable A par une contrainte Ci entraîne la création d'un plan où seront maintenues en séquence les contraintes C1 et C2 par les méthodes sélectionnées. La contrainte C1 est maintenue par l'exécution de la méthode C:=A+B qui modifie la valeur de C, laquelle modification provoque la réévaluation de la contrainte C2 par la méthode E:=B+C. Comme la valeur de B n'est pas modifiée dans cette solution, la contrainte C3 n'est pas réévaluée et aucune de ses méthodes n'apparaît dans le plan.
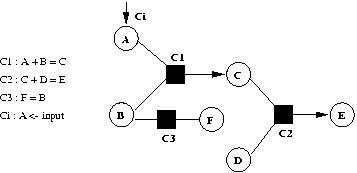
Fig 2. Graphe de solutions
Dans la phase d'exécution, les valeurs connues sont propagées le long des arcs du graphe de solutions obtenu après la phase de planification.
Cette méthode de propagation locale est la plus largement utilisée dans un problème de maintien de solution car elle repose sur une approche incrémentale de la résolution. Là où un résolveur non-incrémental reconsidérerait l'ensemble des contraintes, même en cas de moindre changement, un résolveur incrémental ne réévalue que les contraintes affectées par une perturbation, ce qui lui permet de minimiser le coût d'une nouvelle solution.
[Table des matières]
3.3 Propagation locale par degré de liberté
Il existe une autre méthode de propagation locale qui est la propagation locale par degré de liberté ou PDOFnote1. Une variable possède un degré de liberté d'autant plus grand qu'elle participe à peu de contraintes. Elle est dite libre si elle n'est rattachée qu'à une seule contrainte. Cette définition d'une variable libre est celle généralement adoptée mais elle peut dépendre de l'application et s'appliquer à une variable rattachée à deux contraintes voir plus.
Le principe de la méthode PDOF est de construire le plan dans l'ordre inverse de son exécution, en sélectionnant d'abord les méthodes ayant en sortie des variables libres (le but étant de calculer en dernier les variables les moins contraintes). Lorsqu'une variable libre est trouvée, elle est retirée du graphe de contraintes ainsi que la contrainte qui s'appliquait sur elle. La méthode où la variable apparaissait en sortie est ajoutée au plan. Après ce retrait, une nouvelle variable peut devenir libre et être à son tour retirée. Le processus itère ce traitement jusqu'à ce que le graphe soit vide ou qu'il n'y ait plus de variables libres. Le plan ainsi constitué peut être ensuite exécuté dans l'ordre inverse de sa création pour propager une modification du système de contraintes.
L'exemple de la Fig 3 , donné dans comprend quatre contraintes C1 à C4 et cinq variables A, B, C, D et E (Fig 3 a). L'objectif est de créer un plan pour propager une perturbation de la variable A provoquée par la contrainte C1. La variable E est sélectionnée arbitrairement parmi les trois variables libres C, D et E (a). La variable E et la contrainte C4 sont retirées du graphe, la méthode E := f (B,D) est ajoutée au plan. Le processus itère le même traitement en sélectionnant la variable C (b) puis la variable B (c) en enfin la variable A (d). Il s'arrête quand il n'y a plus de variables libres (e). Le plan constitué pour propager la perturbation correspond au graphe orienté (f).
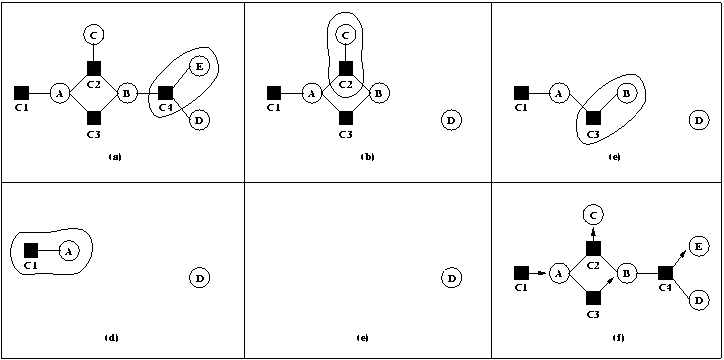
Fig 3. Exemple de propagation locale par degré de liberté
Cette technique a été adaptée par Ivan Sutherland dans son système SketchPad . Elle a ensuite été délaissée, essentiellement à cause du fait qu'elle n'est pas incrémentale. Les récents travaux de Bradley Vander Zanden sur QuickPlan pour la rendre incrémentale l'ont remise au goût du jour.
Après avoir présenté deux méthodes de résolution par propagation locale, nous allons étudier dans cette section quelles sont les caractéristiques principales des résolveurs basés sur ces méthodes. Ces caractéristiques concernent :
[Table des matières]
4.1 Directionnalité
Ce critère caractérise la capacité d'un résolveur à gérer des contraintes unidirectionnelles (one-way) ou multidirectionnelles (multi-way).
Les contraintes unidirectionnelles possèdent une méthode unique de résolution, c'est à dire qu'elles ne peuvent être maintenues que d'une seule façon. Les contraintes multidirectionnelles possèdent au contraire plusieurs méthodes de résolution. Le plus souvent il existe autant de méthodes que de variables intervenant dans la contrainte, ce qui fait que chacune de ces variables peut être déterminée en fonction des autres. Ainsi à la contrainte A+B=C on associera en général trois méthodes : C:=A+B, A:=C-B et B:=C-A. Un exemple d'utilisation de ces deux types de contraintes est illustré Fig 4 . Dans la partie supérieure, le rectangle A et le rectangle B sont alignés sur leur bord gauche par une contrainte unidirectionnelle. L'unique méthode de résolution spécifie que le rectangle B est aligné sur le rectangle A. Si l'on déplace le rectangle A sur l'axe horizontal, alors le rectangle B suit le mouvement de A (la contrainte est maintenue). Si l'on déplace le rectangle B sur l'axe horizontal, le rectangle A reste au contraire immobile. La contrainte d'alignement n'est plus respectée et elle est retirée. Dans la partie inférieure, les deux rectangles sont alignés par une contrainte multidirectionnelle avec deux méthodes de résolution : soit le rectangle A est aligné sur le rectangle B, soit le rectangle B est aligné sur le rectangle A. Le résultat obtenu est que le déplacement de n'importe lequel des deux rectangles entraîne un déplacement analogue de l'autre. La contrainte reste constamment maintenue.
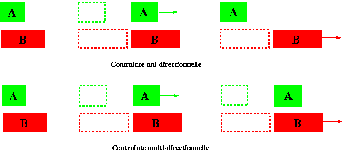
Fig 4. Contrainte unidirectionnelle et multidirectionnelle (1)
Les contraintes multidirectionnelles présentent plusieurs avantages sur les contraintes unidirectionnelles. D'abord elles sont plus générales car une contrainte unidirectionnelle peut toujours être représentée par une contrainte multidirectionnelle pour laquelle on ne définit qu'une méthode de résolution. L'inverse est plus difficile. Par exemple la contrainte A+B=C peut être vérifiée par les trois contraintes unidirectionnelles {C1: C=A+B; C2 : A=C-B et C3 : B=C-A}. La résolution d'un tel problème génère un grand nombre de cycles (Fig 5 a) alors que le même problème avec une contrainte multidirectionnelle C1 : C=A+B est acyclique (Fig 5 b). Or, la gestion des cycles est l'un des problèmes principaux de la propagation locale.
Les contraintes multidirectionnelles sont également plus expressives que les contraintes unidirectionnelles car il est plus simple et plus naturel de présenter ce qui est conceptuellement une seule relation par une seule contrainte plutôt que par plusieurs.
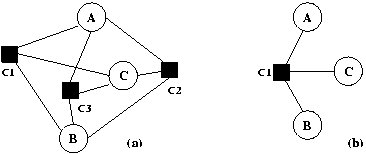
Fig 5. Contrainte unidirectionnelle et multidirectionnelle (2)
En contrepartie, ces avantages ont un coût. Les résolveurs qui gèrent des contraintes unidirectionnelles sont plus efficaces et plus simples à implémenter. En effet, ils doivent trier les contraintes à satisfaire puis les calculer, alors que les résolveurs qui gèrent des contraintes multidirectionnelles doivent en plus choisir une méthode de résolution pour chacune des contraintes à satisfaire. Un autre inconvénient des techniques multidirectionnelles réside dans leur part d'indéterminisme. Sur l'exemple de la contrainte A+B=C, si A est modifiée, alors le résolveur peut choisir de modifier soit B, soit C, soit les deux variables. Il doit donc disposer d'une stratégie de choix appropriée.
[Table des matières]
4.2 Nombre de sorties
Une autre caractéristique des résolveurs de contraintes concerne leur capacité à gérer des contraintes avec sortie unique (one-output) ou sorties multiples (multi-outputs). Une contrainte est à sortie unique si chacune de ses méthodes calcule une variable unique en fonction des autres variables de la contrainte. Une contrainte est à sorties multiples s'il existe au moins une méthode pouvant calculer plusieurs variables en fonction des autres. Bien que la plupart des contraintes "usuelles" ne nécessitent que des méthodes à sortie unique, il est plus simple dans certains cas d'utiliser des méthodes à sorties multiples. Un exemple donné dans est représenté par la relation qui garde cohérentes les coordonnées polaires (rho,theta) et cartésiennes d'un point (x,y). Avec des méthodes à sortie unique (Fig 7 a) cette relation nécessite la définition de quatre contraintes pour calculer chacune des coordonnées. La résolution d'un tel système introduit immédiatement des cycles. Le même exemple avec des méthodes à sorties multiples (Fig 7 b) nécessite la définition d'une contrainte avec deux méthodes, l'une pour calculer rho et theta en fonction de x et y, l'autre pour calculer x et y en fonction de rho et theta (les flèches en dessous de la contrainte représentent ses sorties possibles).
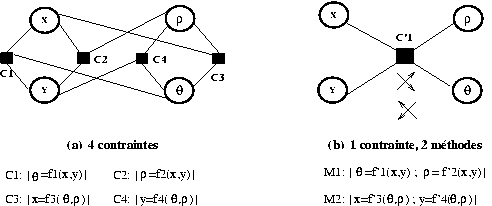
Fig 7. Méthodes avec sortie unique et avec sorties multiples
Les résolveurs qui gèrent des contraintes à sorties multiples sont plus généraux mais des études et des tests (, ) ont montré qu'ils sont plus coûteux en temps et souvent NP-complets.
[Table des matières]
4.3 Stratégies de choix
Une propriété importante des résolveurs de contraintes concerne leur comportement lorsque le système est sur-contraint (aucune solution ne satisfait toutes les contraintes) ou sous-contraint (plusieurs solutions sont possibles).
Dans le cas d'une application interactive, il n'est pas souhaitable de signaler une erreur ou de suspendre la présentation pour demander à l'auteur de choisir une solution. C'est le résolveur qui doit trouver la solution la plus appropriée en ignorant si besoin la définition de certaines contraintes. Une approche proposée dans pour prendre en compte ce problème consiste à gérer une hiérarchie de contraintes. Cette approche fournit un moyen de spécifier de manière déclarative le comportement du résolveur dans les situations précédentes. Pour cela, il est nécessaire de définir une relation d'ordre sur les contraintes et un comparateur.
L'ensemble C des contraintes est partitionné en n+1 sous-ensembles C0,...,Cn de priorité décroissante. La relation d'ordre définit des préférences dans la résolution des contraintes. Les contraintes appartenant au niveau C0 sont les plus fortes. Pour certains résolveurs elles sont obligatoires et leur non-respect provoque un échec de la propagation . Les autres niveaux indiquent un ordre de préférence dans la résolution. Si le résolveur ne peut satisfaire toutes les contraintes, alors il résout d'abord celles de priorité supérieure. Le nombre de niveaux n'est pas fixé, c'est au concepteur du système de déterminer le nombre de niveaux nécessaires, celui-ci ayant une influence sur les performances du résolveur. Un exemple de hiérarchie est proposé par les auteurs avec la définition de cinq niveaux de priorité décroissante : requise pour les contraintes impératives puis forte, moyenne, faible et minimale pour les autres.
Le comparateur comprend une fonction d'erreur qui mesure l'écart entre une solution proposée et la solution qui satisferait l'ensemble des contraintes si cette dernière ne peut être obtenue. Le comparateur peut être de deux types, soit local s'il considère l'erreur pour chaque contrainte à l'intérieur d'un niveau de hiérarchie, soit global s'il considère l'erreur combinée pour chacun des niveaux. La fonction d'erreur quant à elle est de type prédicat ou de type métrique. Dans le premier cas, elle va compter le nombre de contraintes satisfaites ou non satisfaites par niveau de hiérarchie. Dans le second cas, elle va calculer une marge d'erreur à partir des écarts entre les solutions proposées et la satisfaction de l'ensemble des contraintes.
Pour les problèmes de maintien de solution où l'aspect performance est primordial, le comparateur le plus souvent utilisé est le comparateur localement meilleur (locally-predicate-better). Avec celui-ci, on considère les contraintes de façon individuelle en testant uniquement si elles sont satisfaites ou non. Ce comparateur fournit la solution qui vérifie le plus de contraintes possibles au niveau de priorité le plus élevé. Une solution S1 est "meilleure" qu'une solution S2 si S1 vérifie les mêmes contraintes que S2 pour chaque niveau de la hiérarchie jusqu'à un niveau k et au moins une de plus que S2 au niveau k+1. Ce comparateur a le mérite de la simplicité et surtout de l'efficacité mais il peut produire plusieurs "meilleures solutions".
Dans l'exemple de la Fig 8 (a), trois variables A, B et C sont liées par la contrainte requise C1 (C=A+B) qui possède trois méthodes à sortie unique. Une contrainte d'entrée porte également sur chacune des variables pour en déterminer la valeur, C2 sur A (moyenne), C3 sur B (moyenne) et C4 sur C (faible). Ce type de contrainte ne possède qu'une seule méthode de résolution : variable := valeur. Sur la Fig 8 (b), la valeur de A est modifiée par une contrainte forte. Le résolveur construit le plan de propagation correspondant à cette perturbation. La contrainte C2 est retirée car elle est plus faible que la nouvelle contrainte C5, puis la perturbation est propagée sur C1. Comme c'est A qui est modifiée, la perturbation va se propager sur B ou C. Le résolveur peut alors choisir d'appliquer soit la méthode B:=C-A soit la méthode C:=B+A. Pour résoudre ce conflit, il choisit en priorité la méthode qui modifie la variable définie par la contrainte de plus faible poids, soit C dans notre exemple. La méthode C:=B+A est donc choisie pour satisfaire la contrainte C1 et la contrainte C4 est retirée car elle est de plus faible poids que la contrainte C1. Si B et C avaient été définies par des contraintes de même poids, alors il n'y aurait pas eu un choix meilleur que l'autre. C'est alors au résolveur de définir une stratégie pour la propagation.
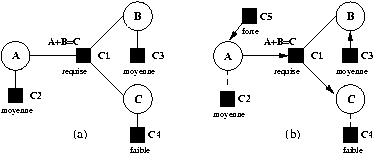
Fig 8. Exemple de hiérarchie de contraintes
[Table des matières]
4.4 Gestion des cycles
Nous avons dit dans la section 3.1.2 que la méthode de résolution par propagation locale ne résout pas les contraintes cycliques, il faudrait pour cela appliquer une méthode globale de résolution qui gère les contraintes de façon simultanée. Prenons l'exemple suivant avec deux contraintes C1 et C2 : {C1: A=B+C; C2: C = B). Trois méthodes à sortie unique sont associées à la première contrainte: A:=B+C, B:=A-C, C:=A-B, deux méthodes à sortie unique sont associées à la deuxième contrainte: C:=B et B:=C. Le graphe de contraintes de cet exemple est donné Fig 9 .
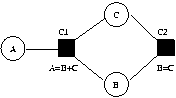
Fig 9. Graphe de contraintes cycliques
Supposons que l'on parte de la solution (A,4), (B,2) et (C,2) et que l'on modifie A avec la valeur 10. Pour maintenir C1, le résolveur doit choisir une méthode où A est une variable d'entrée, soit B:=A-C soit C:=B-A, puis propager la nouvelle modification. S'il choisit B:=A-C, il doit maintenir la contrainte C2 en exécutant une méthode où B est en entrée soit C:=B. La variable C étant modifiée, le résolveur doit de nouveau maintenir la contrainte C1, ce qui crée un cycle. Une solution serait d'arrêter la propagation après un seul parcours de boucle, mais on obtient alors une solution incohérente: (A,10), (B, 8) et (C,8). Si le résolveur avait choisi au départ d'exécuter la méthode C:=A-B le résultat aurait été identique.
Il existe plusieurs stratégies utilisées face à la présence de contraintes cycliques. La plus simple consiste à ne pas les gérer, il faut alors définir des contraintes qui n'introduisent pas de cycles. C'est le cas du résolveur DeltaBlue qui arrête le mécanisme de propagation lorsqu'il détecte un cycle . Une autre stratégie, utilisée notamment par SkyBlue consiste à accepter les cycles et à envoyer la partie cyclique du graphe à un résolveur spécifique. Un problème qui se pose alors est de savoir quelles sont les contraintes à transmettre au résolveur de cycles car, dans certaines situations, il est parfois nécessaire de passer plus de contraintes que celles constituant le cycle afin d'obtenir une solution (section 8.3.1).
[Table des matières]
4.5 Gestion des contraintes d'inégalité
Un critère intéressant pour les résolveurs concerne leur capacité ou non à gérer les contraintes d'inégalité. Ces contraintes arrivent très fréquemment dans le problème du placement spatial. On peut par exemple spécifier qu'un objet A est à gauche d'un objet B ou que des objets A et B doivent rester dans une fenêtre. Or, nous avons vu que la méthode de résolution par propagation locale ne gère que des contraintes de type fonctionnel, c'est à dire des contraintes pour lesquelles chaque variable est déterminée de façon unique en fonction des autres variables de la contrainte. Les contraintes d'inégalité ne sont donc pas des contraintes fonctionnelles.
Certaines extensions ont été proposées pour gérer les inégalités par propagation locale. Parmi celles-ci, nous pouvons citer CobaltBlue , une extension du résolveur SkyBlue utilisée dans CoolDraw, un éditeur graphique à base de contraintes. Dans cet éditeur, une contrainte d'inégalité est représentée par :
A la contrainte A<=10 on associe la méthode A:=10 et une fonction booléenne. Si l'on veut ajouter une telle contrainte à un ensemble de contraintes existantes, on teste au préalable la valeur retournée par la fonction associée. Si la valeur retourne vrai cela veut dire que la contrainte est déjà vérifiée, on ne la prend donc pas en compte. Si la fonction retourne faux et que la contrainte a un poids suffisant, alors elle est prise en compte avec sa méthode fonctionnelle associée. On veut ajouter par exemple la contrainte A<=10 avec un poids fort à un système qui possède déjà une contrainte A=15 de poids faible (cette dernière a positionné la valeur de A à 15). La fonction associée retourne faux car la contrainte A<=10 n'est pas vérifiée. Comme elle a un poids supérieur à la précédente, elle est ajoutée au système avec sa méthode fonctionnelle, si bien que A prend la valeur 10.
Cette extension fonctionne correctement sur des exemples simples mais ne donne pas des résultats satisfaisants sur des problèmes plus complexes. Par exemple, on définit un ensemble de contraintes sur la variable A {faible A=15; forte A<=10; moyenne A<=5}. Si on les introduit dans cet ordre, la valeur de A sera égale à 10 car la troisième contrainte n'est pas prise en compte étant moins forte que la seconde. Or, sa prise en compte eut été préférable car elle aurait permis de satisfaire les deux contraintes les plus fortes (A<=10 et A<=5). Si on les introduit dans l'ordre {faible A=15; moyenne A<=5; forte A<=10}, la valeur de A sera égale à 5. Donc, suivant l'ordre selon lequel on introduit les contraintes on obtient des résultats différents, ce qui est contraire à l'aspect déclaratif des contraintes. De plus, les résultats obtenus ne sont pas toujours les plus pertinents.
Le problème de gestion des inégalités est, avec la gestion des cycles, le deuxième point sur lequel portent les recherches actuelles sur la technique de propagation locale. Des algorithmes utilisant des méthodes de résolution plus globales sont à l'étude .
Nous allons voir dans le paragraphe suivant les critères qui ont guidé notre choix d'un résolveur de maintien de solution pour Madeus.
Dans cette section, nous allons présenter la première sélection que nous avons effectuée sur des résolveurs de maintien de solution pour gérer le placement relatif des éléments dans Madeus.
[Table des matières]
5.1 Présentation de différents résolveurs
Le domaine des algorithmes de maintien de solution, et notamment celui des algorithmes reposant sur la technique de propagation locale est un domaine très actif où beaucoup d'études et de travaux sont menés. Il n'est pas facile d'en avoir une vision synthétique dans le cadre de ce mémoire, c'est pourquoi la liste suivante n'est pas une liste exhaustive. Elle ne cite que quelques uns de ces résolveurs, choisis parmi les plus représentatifs et les plus cités dans le domaine. Chaque article référencé contient de nombreuses autres références sur des travaux annexes.
Un point qu'il est important de noter est qu'actuellement aucun résolveur reposant sur cette technique n'a fait l'objet d'une application commerciale et si de nombreux travaux existent, ils sont tous issus du domaine de la recherche.
Garnet est un environnement de développement d'interfaces utilisateur composé de plusieurs outils (section 0.0.0). Dans le cadre de cette étude, nous ne nous sommes intéressés qu'au mécanisme de résolution de contraintes.
Les contraintes sont représentées par des formules qui définissent la valeur d'une variable (slot) en fonction de la valeur d'autres variables. Chaque contrainte ne possède qu'une méthode de résolution et ne peut donc modifier qu'une seule de ses variables. Cela signifie que les contraintes gérées dans Garnet sont unidirectionnelles (section 4.1), c'est-à-dire que si une variable référencée dans une contrainte change, alors la variable associée à cette contrainte est modifiée, mais l'inverse n'est pas vrai.
Lorsqu'une variable est modifiée, le résolveur recalcule toutes les contraintes où la valeur de cette variable était utilisée. La valeur des variables définies par ces contraintes est donc modifiée, ce qui déclenche le calcul d'autres contraintes et ainsi de suite. La résolution consiste donc en un processus d'évaluation récursive de contraintes et ne nécessite pas la création d'un plan de propagation.
Le résolveur de Garnet gère des contraintes à sortie unique. Il ne maintient pas de hiérarchie de contraintes et ne gère pas les contraintes d'inégalité ni les contraintes cycliques.
Une particularité de ce résolveur est de mettre en oeuvre une évaluation dite paresseuse qui consiste à n'évaluer que les variables qui ont un intérêt pour l'utilisateur. Ainsi, on ne recalcule pas la position d'un objet graphique qui n'apparaît pas à l'écran. Lorsque cet objet doit être affiché, alors l'évaluation des formules calcule sa position correcte.
DeltaBlue a été développé par l'université de Washington à Seattle dans le cadre de ThingLab II, un générateur d'interfaces utilisateur à base de contraintes (0.0.0). Dans ce type d'applications, le point crucial réside dans les performances du résolveur utilisé pour maintenir les contraintes. C'est pourquoi plusieurs algorithmes ont été développés et implémentés afin de tester un "spectre" de techniques de résolution. Le plus performant était l'algorithme DeltaBlue basé sur la technique de propagation locale par valeurs.
DeltaBlue a été l'un des pionniers à utiliser cette méthode et le premier résolveur à utiliser des contraintes multidirectionnelles à sortie unique et à gérer une hiérarchie de contraintes. Par contre, il ne résout pas les cycles ni les contraintes d'inégalité.
DeltaBlue a été développé dans le cadre de ThingLab II mais son aspect général et son aspect novateur font qu'il a été utilisé par la suite dans de nombreuses applications comme "moteur" de résolution . Nous pouvons citer en particulier LayLab , un prototype pour la gestion de présentations multimédia qui utilise DeltaBlue pour résoudre les contraintes d'alignement et d'ordonnancement entre les objets. Nous pouvons également citer les travaux de Louie Weitzman qui définit la présentation de documents à partir de grammaires relationnelles. Une grammaire définit une classe de présentations basée sur des contraintes. Ces contraintes sont ensuite maintenues par DeltaBlue.
SkyBlue a été développé par le même laboratoire que DeltaBlue dans le but d'être un successeur à ce dernier. Comme celui-ci, il repose sur la méthode de propagation locale par valeurs, gère les contraintes multidirectionnelles et une hiérarchie. Mais il est plus général que DeltaBlue car il est capable de traiter des contraintes à sorties multiples et supporte la définition de contraintes cycliques. Cependant, il ne résout pas les cycles lui-même, pour cela il permet de faire appel à des résolveurs externes spécifiques. Nous avons également vu à la section 4.5, une extension de SkyBlue, appelée CobaltBlue, qui propose une solution pour gérer les contraintes d'inégalité.
Comme DeltaBlue, SkyBlue est un résolveur général utilisé dans de plusieurs applications et notamment dans TBAG 3D, un système d'animation, VB2 un système de réalité virtuelle et PIKA un système de simulations. Nous avons également cité précédemment deux applications qui utilisent SkyBlue, Kaleidoscope (0.0.0), un langage intégrant la programmation impérative et la programmation déclarative à base de contraintes et CoolDraw , un éditeur graphique à base de contraintes qui utilise CobaltBlue.
L'application ICOLA (section 0.0.0) comprend un résolveur de contraintes, une interface graphique et de nombreuses librairies . Seul le mécanisme de résolution incrémentale de contraintes a été étudié pour notre problème.
Le résolveur de contraintes d'ICOLA repose sur la technique de propagation locale par valeurs et gère des contraintes multidirectionnelles avec sortie unique. Il ne maintient pas de hiérarchie de contraintes mais utilise deux heuristiques lorsque le système est sous-contraint (plusieurs solutions sont alors possibles). La première de ces heuristiques est appliquée en priorité et indique que les objets doivent être le plus proche possible de l'origine de l'image affichée. La seconde heuristique impose à chaque objet de tendre vers sa taille minimale. La première heuristique est également appliquée pour les contraintes d'inégalité afin de choisir une valeur unique pour une variable.
Le résolveur de contraintes d'ICOLA ne maintient pas les contraintes cycliques. Pour éviter de construire un graphe cyclique, il effectue préalablement un contrôle de cohérence lorsqu'une contrainte est ajoutée (dans ICOLA, la suppression d'une contrainte ne génère pas de cycle). Lors de l'ajout d'une contrainte entre deux variables x et y, le résolveur vérifie d'abord s'il existe un chemin dans le graphe de contraintes entre ces deux variables. S'il en existe un, alors la contrainte est refusée. S'il n'existe pas de chemin entre x et y, alors la contrainte est acceptée et maintenue.
Ce résolveur est spécifique à ICOLA et n'a pas été utilisé dans d'autres applications.
QuickPlan est un algorithme récent de résolution de contraintes développé par Bradley Vander Zanden . Il est proche de SkyBlue dans le sens où il gère des contraintes multidirectionnelles avec sorties multiples et une hiérarchie de contraintes. La différence vient du fait qu'il utilise une méthode de résolution incrémentale qui repose sur la propagation locale par degré de liberté (3.3).
La particularité de QuickPlan (et de l'approche PDOF en général) est de ne construire que des graphes de solutions acycliques. Il ne permet pas de résoudre les cycles mais il est capable de trouver une solution acyclique, s'il en existe une, dans un graphe de contraintes potentiellement cyclique. Sur l'exemple de la Fig 10 , le graphe de contraintes (a) est potentiellement cyclique puisqu'il existe au moins une solutions contenant un cycle (b). S'il existe une solution ne contenant pas de cycle (c), alors QuickPlan peut la trouver.
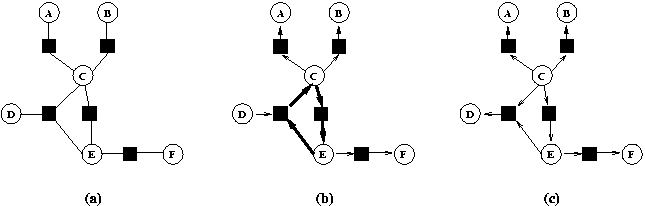
Fig 10. Recherche de solution acyclique par QuickPlan
Comme les résolveurs précédents, QuickPlan ne gère pas les contraintes d'inégalité.
Aucune implémentation de l'algorithme QuickPlan n'est actuellement disponible.
Le résolveur UltraViolet est développé par l'équipe du professeur Borning à l'origine de DeltaBlue et SkyBlue. Ses auteurs sont partis du constat que la propagation locale est une technique très performante mais qu'elle ne peut apporter des solutions aux problèmes des cycles et des inégalités. Or ce sont des problèmes qui arrivent très fréquemment dans le domaine des interfaces utilisateur. D'un autre côté, les algorithmes qui proposent des solutions à ces problèmes ne sont développés que pour des types de données bien spécifiques et sont beaucoup moins performants. L'idée à l'origine d'UltraViolet était de créer un résolveur hybride qui utilise la propagation locale tant qu'elle peut s'appliquer et des techniques plus globales pour les problèmes de cycles et d'inégalités. La structure modulaire d'UltraViolet permet d'intégrer différents résolveurs, actuellement au nombre de quatre :
Pour permettre à ces différents résolveurs de travailler ensemble, le graphe de solution est partitionné en régions cycliques et acycliques puis, pour ces dernières, en régions contenant des contraintes numériques ou non. Chaque résolveur travaille ensuite exclusivement sur les régions du graphe qui le concernent, la communication entre eux se faisant par l'intermédiaire de variables partagées.
Dans le cadre de ce mémoire, nous ne présenterons que le résolveur Indigo.
Indigo est similaire à DeltaBlue par de nombreux aspects (gestion de contraintes multidirectionnelles à sortie unique, gestion d'une hiérarchie de contraintes), mais il est capable de résoudre en plus les contraintes d'inégalités portant sur des variables numériques. Pour cela, il utilise un mécanisme de propagation qui agit non pas sur des valeurs mais sur des intervalles de valeurs.
Initialement, toutes les variables du système possèdent l'intervalle (ou domaine) de valeurs ]-infty, +infty[. Indigo considère ensuite chaque contrainte du système par ordre de priorité décroissante. La prise en compte d'une contrainte a pour effet de réduire le domaine de valeurs de sa variable de sortie, cette modification étant ensuite propagée pour réduire le domaine de valeurs d'autres variables du système en fonction des contraintes précédemment traitées. L'état final du système correspond à une solution où chaque variable possède un domaine de valeurs réduit à un singleton. Il est à noter que toutes les variables possèdent automatiquement, à leur création, une contrainte de maintien de valeur de priorité minimale qui a pour effet d'affecter une valeur à la variable associée. Comme ces contraintes sont de priorité minimale, elles sont traitées en dernier et permettent de réduire à une valeur unique les domaines qui ne le seraient pas encore.
Un exemple d'utilisation d'Indigo est donné dans . Considérons les contraintes suivantes :
(1) a >= 10 requise (2) b >= 20 requise (3) a + b = c requise (4) c + 25 = d requise (5) d <= 100 forte (6) a = 50 moyenne (7) a = 5 minimale (8) b = 5 minimale (9) c = 100 minimale (10) d = 200 minimale
Les contraintes sont traitées par ordre de priorité décroissante. Le traitement de a >= 10 réduit le domaine de a à [10, +infty[, celui de b >= 20 réduit le domaine de b à [20, +infty[. Le traitement de a + b = c réduit le domaine de c à [30, +infty[, celui de c + 25 = d réduit le domaine de d à [55, +infty[. Indigo traite ensuite la contrainte forte d <= 100 qui modifie de domaine de d à [55, 100]. Cette modification est propagée sur c [30, 75] (3) puis sur a [10, 55] et enfin sur b [20, 65] (2). La contrainte moyenne a = 50 réduit les domaines de a [50 50], puis par propagation ceux de b [20, 25], c [70, 75] et d [95, 100]. Finalement, les contraintes de priorité minimale sont traitées. La contrainte a = 5 n'a aucun effet puisque le domaine de a est déjà réduit à une valeur unique. La satisfaction de b = 5 est également impossible puisque la valeur 5 n'est pas dans le domaine courant de b. Néanmoins, Indigo réduit le domaine de b au singleton [20, 20] (qui est la moins mauvaise valeur pour la contrainte b = 5) et propage cette modification aux domaines de c [70, 70] et d [95, 95]. Les deux autres contraintes minimales n'ayant aucun effet, la solution est finalement a=50, b=20, c=70 et d=95.
Cet algorithme de propagation sur des intervalles propose un traitement intéressant des contraintes d'inégalité mais présente toutefois l'inconvénient d'être difficilement incrémental. En effet, l'ajout ou le retrait d'une contrainte oblige le résolveur à reconsidérer toutes les contraintes existantes (en particulier, le retrait d'une contrainte ne peut relâcher le domaine d'une variable que si le résolveur traite de nouveau toutes les contraintes sur cette variable). Par conséquent, ses performances ne sont pas aussi intéressantes que celles d'autres résolveurs et en particulier des résolveurs précédents qui utilisent tous des techniques incrémentales.
[Table des matières]
5.2 Tableau de synthèse
Le tableau suivant récapitule les caractéristiques mises en relief dans la section 4 pour les différents résolveurs de maintien de solution que nous venons de présenter.
| Directionnalité | Hiérarchie de contraintes | Nombre de sorties | Acceptation des cycles | Gestion des inégalités | |
|---|---|---|---|---|---|
| DeltaBlue | Multi | Oui | Une | Non | Non |
| SkyBlue | Multi | Oui | Multi | Oui | Non |
| ICOLA | Multi | Non | Une | Non | Non |
| Garnet | Une | Non | Une | Non | Non |
| QuickPlan | Multi | Oui | Multi | Oui | Non |
| Indigo | Multi | Oui | Une | Non | Oui |
[Table des matières]
5.3 Critères de sélection
Nous avons défini deux catégories de critères, ceux qui correspondent aux caractéristiques intrinsèques du résolveur et ceux qui concernent son utilisation de façon plus générale.
Les caractéristiques que nous voulons obtenir de la part du résolveur correspondent à nos besoins en termes de relations spatiales.
D'abord, le fait de vouloir des relations symétriques induit que le résolveur doit gérer des contraintes multidirectionnelles. Cette caractéristique correspond à un critère impératif pour notre choix.
Ensuite, les relations du style A_gauche_de, En_dessous_de ainsi que le fait qu'un élément doit rester à l'intérieur de son élément composite font que le résolveur doit résoudre des contraintes d'inégalité. De plus, les configurations spatiales que nous voulons obtenir induisent fréquemment des cycles, par exemple (Fig 12 ), en spécifiant des relations d'Alignement_Gauche entre deux éléments A et B (C1) puis, entre deux éléments B et C (C2) et enfin, entre les éléments A et C (C3). Il est donc intéressant que le résolveur puisse résoudre des systèmes de contraintes cycliques ou tout du moins en accepter la définition. Cependant, nous avons vu que ces deux derniers critères correspondent aux limitations actuelles de la propagation locale, c'est pourquoi nous ne les considérerons pas comme des critères obligatoires.
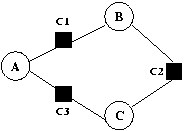
Fig 12. Relations générant un cycle
Enfin, l'aspect performance du résolveur sélectionné est également important pour notre projet, notamment pour le déplacement continu des éléments.
L'objectif de cette étude est de sélectionner un algorithme de maintien de solution déjà implémenté dans un langage compatible avec l'application Madeus (écrite en C). Un des critères impératifs de notre choix est donc la disponibilité des sources du résolveur.
De plus nous cherchons un résolveur indépendant qui peut être utilisé sans contexte applicatif.
Un autre critère qui nous paraît important dans le choix d'un résolveur concerne sa diffusion et son utilisation dans différents types d'applications, ce qui permet d'avoir des études supplémentaires et des retours éventuels d'utilisateurs.
Enfin, on s'intéressera plus à un résolveur qui continue à être l'objet de recherches qu'à un résolveur dont les évolutions sont arrêtées.
[Table des matières]
5.4 Première sélection
Nous avons fait une première sélection fondée sur l'étude théorique des résolveurs présentés dans la section 5 et sur leur correspondance aux critères précédemment définis :
De ce fait, notre choix s'est porté sur les résolveurs DeltaBlue et SkyBlue et ce pour plusieurs raisons.
D'abord, les sources de ces résolveurs sont disponibles en langage C et sont directement compatibles avec l'application Madeus.
Ensuite, ce sont des résolveurs généraux qui n'ont pas été développés pour un type d'application particulière. De plus, ils ont l'avantage d'être déjà utilisés dans plusieurs applications et notamment dans des applications graphiques et de posséder une "documentation" facilement disponible.
Enfin les travaux de l'équipe du professeur Borning ont été novateurs dans ce domaine et beaucoup de recherches utilisent leurs résultats. De plus, cette équipe travaille toujours sur la technique de propagation locale et ses recherches récentes concernent l'évolution des techniques de propagation locale afin de traiter certaines de leurs limitations.
Dans les prochaines sections nous allons présenter plus en détail ces deux résolveurs. Nous présenterons d'abord DeltaBlue qui a été le premier résolveur de ce laboratoire, puis les améliorations apportées par SkyBlue. Nous préciserons ensuite le choix final effectué entre les deux.
DeltaBlue gère des contraintes multidirectionnelles avec sortie unique. Il intègre une hiérarchie de contraintes avec plusieurs niveaux de priorités (ou poids) prédéfinis par l'utilisateur. Le niveau le plus élevé regroupe les contraintes impératives. Une contrainte de ce niveau qui ne peut être satisfaite aboutit à un échec de la propagation. La hiérarchie de contraintes définie dans DeltaBlue est la suivante, par ordre de poids décroissant : requise, forte, moyenne, faible, minimale.
[Table des matières]
6.1 Poids de parcours
L'idée générale de DeltaBlue est d'associer à chaque variable du graphe de contraintes une information suffisante pour permettre au résolveur de choisir la façon de satisfaire une contrainte en examinant simplement les variables de celle-ci. Cette information, appelée poids de parcours (walkabout strenght) sert à propager dans le graphe des informations liées au niveau de priorité des contraintes. Elle prend donc une valeur parmi les valeurs définies pour le poids des contraintes.
Le poids de parcours d'une variable V est mis à jour automatiquement par le résolveur de la manière suivante :
L'exemple de la Fig 13 comprend quatre variables A, B, C, D et quatre contraintes C1, C2, C3, C4 de poids respectif forte, requise, requise et faible. Les flèches sur les arcs indiquent les entrées et la sortie des méthodes utilisées dans la solution courante. Les variables sont étiquetées avec leur poids de parcours. Celui de A et celui de B sont définis par le poids de la contrainte qui les détermine, ils sont respectivement à forte et requise. Le poids de parcours de la variable C est égal au minimum entre le poids de la contrainte C3 (requise) et le poids de parcours des variables d'entrées de celles-ci dans la solution courante à savoir A et B. Il est donc égal à forte. De la même manière, le poids de parcours de la variable D est égal au minimum entre le poids de la contrainte C4 et le poids de parcours des variables d'entrée de celle-ci. Il est donc égal à faible.
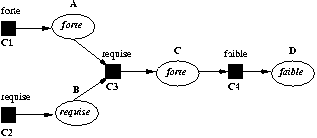
Fig 13. Calcul du poids de parcours
Les poids de parcours reflètent, pour chaque variable le poids de la plus faible contrainte qui influence sa valeur. Sur l'exemple précédent, le poids de parcours de la variable C est positionné à forte à cause de la contrainte C1 sur la variable A. Cette contrainte peut être "éloignée" de la variable dans le graphe de contraintes et c'est précisément l'utilité des poids de parcours que d'encapsuler une information que sinon Deltablue devrait acquérir en parcourant le graphe entier. Grâce à l'information portée par les poids de parcours, le résolveur connaît, pour une variable, le poids de la plus faible contrainte qui peut être relâchée pour satisfaire une contrainte plus forte sur cette variable (sections 6.4.3 et 6.4.4).
[Table des matières]
6.2 Structures de données
DeltaBlue manipule plusieurs structures de données pour maintenir une solution courante. Parmi celles-ci, nous trouvons les structures correspondant aux variables, aux contraintes et aux méthodes utilisées.
Une variable n'est pas assimilée à une valeur mais à une structure (Fig 14 ) dont la valeur ne représente qu'un champ. En plus de sa valeur, une variable DeltaBlue garde une trace de toutes les contraintes qui la référencent (Contraintes) et un pointeur particulier sur la contrainte qui détermine sa valeur dans la solution courante (DéterminéePar). Si aucune contrainte ne détermine la valeur de la variable, ce champ possède la valeur "aucune". Le champ PoidsLocal correspond au poids de parcours que nous avons présenté dans la section précédente. Le champ Marque est utilisé par DeltaBlue lors de la sélection de méthodes et lors de la propagation. Il sert en particulier à détecter les cycles.
Lors de sa création, une variable est déterminée par une contrainte virtuelle de poids minimal.
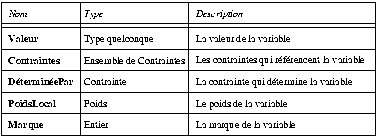
Fig 14. Structure d'une Variable DeltaBlue
La structure Contrainte (Fig 15 ) définit une contrainte qui porte sur un ensemble de variables (Variables). Le champ Méthodes contient l'ensemble des méthodes définies pour satisfaire la contrainte. Le champ MéthodeSelectionnée référence la méthode utilisée pour satisfaire la contrainte dans la solution courante. Si la contrainte n'est pas satisfaite, ce champ contient la valeur "aucune". Le champ ContrainteEntrée est à "vrai" pour une contrainte d'entrée. Une contrainte d'entrée est une contrainte qui affecte une valeur à une variable, elle ne possède qu'une méthode de résolution qui est : variable <- valeur. Enfin, le champ Poids contient le poids de la contrainte dans la hiérarchie.

Fig 15. Structure d'une Contrainte DeltaBlue
Une méthode représente une des façons potentielles de satisfaire une contrainte. La structure Méthode (Fig 16 ) comprend deux champs, une procédure à appliquer (Code) et une référence sur la variable de sortie de la méthode (Sortie). C'est cette variable qui est modifiée par l'application de la procédure. La procédure contient également les références sur les variables d'entrée utilisées par la méthode.

Fig 16. Structure d'une Méthode DeltaBlue
[Table des matières]
6.3 Définition des contraintes
Du point de vue de la définition de contraintes, DeltaBlue présente l'avantage d'être un système "souple" où les règles de propagation, c'est-à-dire les méthodes de résolution associées aux contraintes, sont séparées du mécanisme de propagation lui-même. La définition de nouvelles contraintes s'en trouve donc facilitée car l'auteur a juste à spécifier les méthodes associées. De même c'est un système général qui n'est pas limité aux contraintes numériques. D'autres types de contraintes peuvent être définies, ce sont les méthodes associées qui fournissent le mécanisme de résolution. On peut par exemple définir une contrainte entre le libellé d'une police de caractères et l'affichage de celui-ci avec les caractéristiques de la police. Les méthodes de cette contrainte doivent appeler des fonctions système pour retrouver la police de caractères dans les répertoires correspondants, isoler ses caractéristiques et les affecter au libellé.
DeltaBlue définit certaines contraintes "de base" comme par exemple les contrainte d'égalité ou de somme. La contrainte d'égalité est schématisée Fig 17 . Elle porte sur deux variables A et B et stipule que leurs valeurs restent constamment égales. Si la valeur de A est modifiée, alors la valeur de B l'est en conséquence (méthode 1) et inversement (méthode 2).
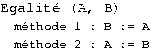
Fig 17. Contrainte d'égalité
La contrainte de somme porte sur trois variables (Fig 18 ). Elle stipule qu'une variable Sum est égale à la somme des variables A et B. Trois méthodes sont définies pour calculer chacune des variables en fonction des deux autres.
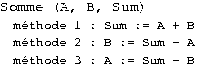
Fig 18. Contrainte de somme
Lorsqu'une variable est modifiée, une ou plusieurs contraintes peuvent ne plus être satisfaite(s). Pour satisfaire une contrainte, DeltaBlue choisit puis exécute l'une des méthodes associées parmi celles où la variable modifiée est en entrée.
Un point à noter dans la définition des contraintes par DeltaBlue est que ce dernier ne gère pas de priorité entre les méthodes à l'intérieur d'une même contrainte. En particulier, il ne précise pas quelle méthode doit être utilisée lorsqu'il y a un conflit entre plusieurs méthodes possibles. Sur la contrainte de somme précédente (Fig 18 ), une modification de la variable A peut provoquer soit l'exécution de la méthode 1 (Sum est alors modifiée), soit l'exécution de la méthode 2 (B est alors modifiée). En fait, c'est l'ordre de définition des méthodes qui détermine ce choix. Une étude a été menée afin d'orienter le choix d'une méthode de résolution plutôt qu'une autre lorsqu'il y a conflit . Dans cette étude, le choix est fonction du nombre de contraintes à réévaluer pour chacune des possibilités. Mais cette éventualité n'est pas satisfaisante car elle ne reflète pas un choix de l'auteur.
[Table des matières]
6.4 Fonctionnement
L'interface entre DeltaBlue et le programme "client" s'effectue à travers quatre points d'entrée :
Les variables doivent être préalablement définies avant d'être utilisées dans des contraintes. Elles sont créées avec une contrainte virtuelle de poids minimal. L'ajout d'une variable dans le graphe de contraintes n'a pas d'effet sur la solution courante.
Une variable est supprimée en deux étapes. D'abord, toutes les contraintes qui la référencent sont retirées du graphe (section 6.4.4). Ensuite la variable elle-même est supprimée.
Pour satisfaire une contrainte C, DeltaBlue utilise les poids de parcours des variables. Il essaie de trouver une méthode associée à C dont la variable de sortie a un poids de parcours plus faible que le poids de la contrainte C. Si tel est le cas, alors la méthode associée à la contrainte C est prise en compte et la méthode qui déterminait précédemment cette variable de sortie n'est plus appliquée. La contrainte à laquelle était associée cette dernière méthode est relâchée, c'est-à-dire qu'elle n'est plus vérifiée dans la solution courante (elle possède un poids inférieur à celui de la contrainte C). La contrainte C est marqué satisfaite et le poids de parcours de ses variables aval dans le graphe est recalculé. Si une telle méthode ne peut être trouvée, cela signifie que C ne peut être satisfaite sans relâcher une contrainte de poids supérieur ou égal à celui de C. Relâcher une contrainte de même poids peut conduire à une solution différente mais pas "meilleure" selon le comparateur utilisé (prédicat localement meilleur). Relâcher une contrainte de poids supérieur conduirait à une solution moins bonne que la solution courante.
L'exemple de la Fig 19 montre le processus d'ajout d'une contrainte dans une solution initiale (a). Le poids de parcours de la variable D est égal à faible, cela reflète l'existence dans le graphe d'une contrainte amont de poids faible (dans l'exemple, il s'agit de la contrainte C2 entre les variables A et B). On ajoute une contrainte de poids forte sur D (b). Cette contrainte peut être satisfaite parce que son poids est supérieur au poids de parcours de la variable D. DeltaBlue retire la contrainte qui déterminait précédemment D, la contrainte C4 entre les variables C et D et met à jour le poids de parcours de la variable D (c). Il itère le traitement en considérant maintenant la contrainte retirée C4. Comme son poids (requise) est supérieur au poids de parcours de chacune de ses variables (faible pour C et forte pour D), elle peut être satisfaite. DeltaBlue choisit toujours de modifier la variable de plus faible poids, à savoir C. Ceci a pour conséquence de retirer la contrainte C3 qui déterminait précédemment la variable C et de mettre à jour le poids de parcours de celle-ci à forte (d). Le processus de propagation continue de la même manière jusqu'à retirer la contrainte responsable du poids de parcours initial de D (C2). Cette contrainte n'a pas un poids suffisant pour être satisfaite et le processus de propagation s'arrête (e).
Lors de l'ajout d'une contrainte, le processus de propagation peut échouer dans les deux cas suivants :
Dans les deux cas la propagation est arrêtée et un message d'erreur est envoyé à l'utilisateur.
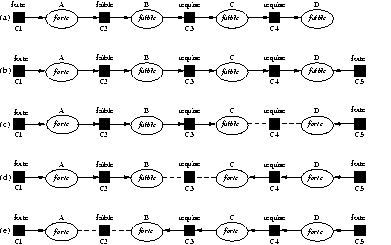
Fig 19. Ajout d'une contrainte
Si la contrainte à retirer n'est pas satisfaite dans la solution courante, alors son retrait n'induit aucune modification dans celle-ci. Si au contraire elle est satisfaite, le traitement est plus complexe. En effet, le retrait d'une contrainte peut modifier le poids de parcours de variables aval de celle-ci et permettre ainsi qu'une ou plusieurs contrainte(s) non satisfaite(s) dans la solution courante le devienne(nt).
Dans l'exemple de la Fig 20 , on veut supprimer la contrainte C6, de poids forte, qui détermine la variable D (a). On note que la contrainte C2 (faible) entre les variables A et B et la contrainte C5 (moyenne) entre les variables C et D ne sont pas satisfaites car leur poids est inférieur au poids de parcours de leurs variables. La suppression de la contrainte C6 entraîne le calcul du poids de parcours de ses variables avals (les variables D et B dans la première configuration). Comme D n'est plus déterminée par aucune contrainte, son poids de parcours est minimale. Celui-ci entraîne la modification du poids de parcours de B à minimale également (b). Les contraintes C2 et C5 non satisfaites jusqu'alors ont toutes les deux maintenant un poids supérieur à l'une de leur variable. Le résolveur peut donc les satisfaire. Dans ce cas, DeltaBlue satisfait d'abord la contrainte de plus fort poids à savoir C5. Ceci a pour conséquence de mettre à jour le poids de parcours des variables D puis B (c). DeltaBlue essaie alors de satisfaire la dernière contrainte "en attente", C2, mais étant donné que le poids de cette dernière (faible) est inférieur au poids de parcours de chacune de ses variables, elle reste non satisfaite. Comme aucune autre contrainte n'est à considérer, DeltaBlue arrête le processus de propagation.
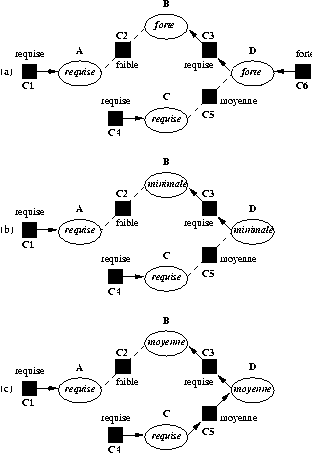
Fig 20. Retrait d'une contrainte
Pour satisfaire une contrainte répétitive comme par exemple le déplacement d'un objet à la souris, DeltaBlue permet de créer un plan de propagation à partir de la contrainte spécifiée. Ce plan mémorise la séquence de méthodes à exécuter pour propager la perturbation provoquée par l'application de la contrainte. Il peut être ensuite exécuté par une procédure distincte qui considère chaque méthode de ce plan en séquence et applique la procédure qui lui est associée. Tant que le graphe de solution n'est pas changé par l'ajout ou le retrait d'une contrainte, le plan constitué peut être exécuté pour propager de nouvelles valeurs. Lorsque le graphe change, le plan devient invalide.
[Table des matières]
6.5 Résultats - Complexité
Pour un graphe de contraintes acyclique, l'appel des procédures d'ajout et de suppression d'une contrainte est dans le pire des cas en O(MN) où N représente le nombre total de contraintes dans le graphe et M le nombre maximum de méthodes définies pour une contrainte . Dans la plupart des applications, M est borné par une constante relativement faible, 3 ou 4 en général. Cela signifie que le coût de l'algorithme est linéaire en fonction du nombre de contraintes, ce qui le rend particulièrement performant.
Plusieurs jeux de tests sont présentés dans . L'un d'eux consiste à ajouter une contrainte à l'une des extrémités d'une longue chaîne de contraintes d'égalité : V1 = V2, V2 = V3, ..., Vn-1 = Vn (Fig 21 ). Ces contraintes sont bidirectionnelles et de poids requise. Une contrainte de poids faible est appliquée à Vn pour s'assurer que la propagation s'effectue de Vn vers V1 (a). On ajoute ensuite une contrainte de poids forte sur la variable V1, ce qui a pour conséquence de renverser complètement la propagation (b). Chaque contrainte de la chaîne doit être examinée lors de cet ajout.
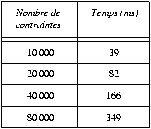
Fig 21. Jeu de test sur une chaîne de contraintes
Le tableau suivant montre les performances mesurées sur notre station de travail (station Sun UltraSPARC-1 à 146 MHz, système Solaris 2.5). Les durées correspondant au temps nécessaire pour l'ajout de la contrainte forte dans une chaîne de n contraintes. Il est à noter que le temps de propagation croît de façon linéaire en fonction du nombre de contraintes.
| Nombre de contraintes | Temps (ms) | Nombre de contraintes | Temps (ms) |
|---|---|---|---|
| 100 | 1 | 10 000 | 39 |
| 500 | 2 | 20 000 | 82 |
| 1 000 | 4 | 40 000 | 166 |
| 5 000 | 20 | 80 000 | 349 |
Le second résolveur que nous allons étudier est SkyBlue. Il a été développé dans le but d'être le successeur de DeltaBlue. Comme ce dernier, il utilise la propagation locale par valeurs, résout les contraintes multidirectionnelles et gère une hiérarchie de contraintes. Mais il l'améliore sur deux points principaux qui sont la gestion des contraintes à sorties multiples et le maintien de contraintes générant des cycles. Ce sont ces deux aspects que nous allons présenter dans la suite de cette section.
[Table des matières]
7.1 Contraintes à sorties multiples
Nous avons vu dans la section 4.3 qu'une contrainte à sorties multiples est une contrainte dont au moins une méthode possède plusieurs variables de sortie. Nous avons vu également un exemple d'utilisation de telles contraintes pour le maintien de la cohérence entre les coordonnées polaires et cartésiennes d'un point.
Néanmoins, la plupart des systèmes peuvent se concevoir en utilisant uniquement des contraintes à sortie unique (ce qui est notre cas). De plus, la spécification de contraintes à sorties multiples alourdit la tâche du programmeur. En effet, sur l'exemple de la contrainte C=A+B, on peut vouloir définir des méthodes pour répercuter la modification d'une variable sur les deux autres (Fig 23 ). On peut en plus vouloir spécifier des méthodes à sortie unique pour satisfaire cette contrainte, ce qui multiplie le nombre de méthodes possibles et donc l'éventail du choix pour satisfaire une contrainte.
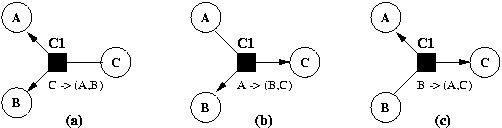
Fig 23. Exemple de méthodes à sorties multiples
Un problème qui se pose également avec ce type de contraintes est de spécifier la répartition de la modification d'une variable sur les autres. Sur l'exemple précédent, si on part d'une solution courante (A,5), (B,2), (C,7) et que l'on affecte C à 11, il y a plusieurs façons de modifier A et B : (A,6) et (B,5), (A,7) et (B,4), (A,8) et (B,3). Il revient à l'utilisateur de SkyBlue de définir le comportement unique de chaque méthode.
[Table des matières]
7.2 Spécification de contraintes cycliques
L'apport le plus important de SkyBlue par rapport à DeltaBlue réside dans l'acceptation de contraintes qui génèrent des cycles. SkyBlue ne résout pas lui-même les cycles mais permet d'isoler les parties cycliques du graphe de solutions et permet de les envoyer à des résolveurs spécifiques qui ne reposent pas sur le principe de propagation locale.
Sur l'exemple de la Fig 24 (a), les méthodes sélectionnées pour les contraintes C2 et C3 forment un cycle. Le cycle est réduit de façon à traiter les contraintes comme s'il y avait une méthode unique qui lisait la variable V2 et affectait les variables V3 et V4 avec des valeurs qui satisfassent les deux contraintes (b). Ce schéma n'est valable que si la méthode associée au cycle peut délivrer plusieurs sorties, d'où la nécessité de disposer de méthodes à sorties multiples. Lorsque ce traitement a été effectué pour tout le graphe, les méthodes sont exécutées selon l'ordre topologique. Les méthodes "normales" sont traitées par le mécanisme de propagation locale. Lorsqu'un cycle est rencontré, SkyBlue fait appel à un ou plusieurs résolveurs externes qui tentent de trouver des valeurs pour les variables de sortie du cycle, afin de satisfaire les contraintes. Si le cycle est résolu, alors les valeurs sont propagées dans le reste du graphe. Si aucun résolveur ne peut résoudre le cycle ou que l'un d'eux stipule que le cycle ne peut être résolu, alors les variables du cycle ne sont pas modifiées et les méthodes et cycles suivants ne sont pas exécutés. Les variables en aval du cycle non résolu sont marquées spécifiquement de sorte que l'utilisateur de SkyBlue peut savoir que leur valeur ne satisfait pas les contraintes.
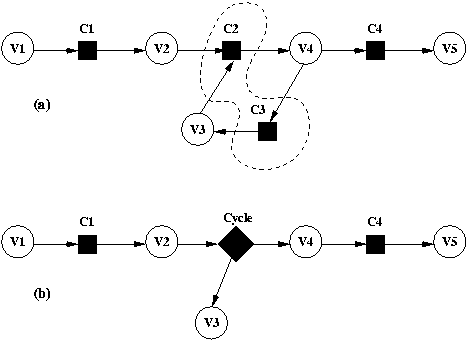
Fig 24. Principe de maintien de contraintes cycliques dans SkyBlue
Les résolveurs externes sont en général spécifiques pour un type de variables donné. Si par exemple toutes les contraintes sont des équations linéaires, alors SkyBlue appellera un résolveur qui incorpore un mécanisme de résolution simultanée d'équations linéaires. Autant de résolveurs que nécessaires peuvent être appelés selon la nature des contraintes mises en jeu.
La version disponible de SkyBlue n'intègre pas de tels résolveurs. La solution pour pouvoir tester complètement SkyBlue serait d'écrire soi-même ces résolveurs ou bien d'en trouver qui conviennent pour certains types de variables (variables numériques par exemple) et de les connecter avec SkyBlue. La première éventualité sort du cadre de ce mémoire. La seconde éventualité représente un travail coûteux pour la recherche et surtout pour l'interfaçage de ces résolveurs avec les procédures d'appel de SkyBlue. De plus, nous verrons dans la section 8.3.1 que la collaboration avec des résolveurs externes nécessite une approche plus globale que celle adoptée par SkyBlue. Pour toutes ces raisons, nous n'avons pas testé SkyBlue avec des résolveurs de cycles externes.
[Table des matières]
7.3 Résultats - Complexité
Le fonctionnement de SkyBlue est plus complexe que celui de Deltablue car il doit gérer des situations supplémentaires. Notamment, le calcul incrémental du poids de parcours de chaque variable doit tenir compte des sorties multiples et des cycles .
Nous avons comparé les performances de DeltaBlue et SkyBlue sur l'exemple de la chaîne de contraintes vu en 6.5 (sur la même station de travail et dans des conditions identiques). Cet exemple n'est pas représentatif de SkyBlue car il ne comprend ni cycles ni méthodes à sorties multiples, néanmoins il permet de faire une première comparaison sur des actions identiques. Avec SkyBlue, nous constatons que le temps nécessaire pour l'ajout de la contrainte forte est beaucoup plus élevé que pour DeltaBlue et qu'il ne progresse pas de façon linéaire en fonction du nombre de contraintes comme pour ce dernier.
| Nombre de contraintes | Temps (ms) | Nombre de contraintes | Temps (ms) |
|---|---|---|---|
| 50 | 5 | 1 000 | 240 |
| 100 | 9 | 1 500 | 398 |
| 500 | 77 | 2 000 | 647 |
Des tests plus complets , montrent que dans le pire des cas les performances sont exponentielles en O(MN) où N est le nombre de contraintes et M le nombre maximal de méthodes par contrainte. Ces références montrent qu'un problème de résolution avec cycles et sorties multiples est NP-complet.
La sélection finale du résolveur a été faite à partir de leur étude théorique mais aussi à partir de tests sur une première implémentation. Celle-ci consiste en une interface graphique où l'utilisateur manipule des objets sous forme de boîtes. Ils sont caractérisés par six paramètres : le bord gauche, le bord droit, le bord supérieur, le bord inférieur et les deux dimensions. L'ensemble de ces paramètres représente les variables du système de contraintes. Les objets sont liés entre eux par des contraintes sur leur position ou leurs dimensions relatives. Les contraintes sont exprimées de façon statique avant l'exécution. En l'absence de contraintes, les objets ont un positionnement par défaut. Les actions possibles sur les objets sont le déplacement et le redimensionnement.
[Table des matières]
8.1 Tests sur un prototype de placement de boîtes
Dans l'exemple de la Fig 25 , nous avons exprimé les contraintes suivantes :
Rouge Aligné-Haut Bleue
Rouge Même-Hauteur Bleue
Verte A-Droite-De(0) Rouge
Jaune Centré-Vertical Orange
Mauve En-Dessous-De Grise
Les contraintes sur les objets sont traduites sous forme de contraintes sur leurs variables. Ainsi,"Rouge Aligné-Haut Bleue" est transformée en contrainte Rouge.haut = Bleue.haut et "Verte A-Droite-De(0) Rouge" est transformée en contrainte Verte.gauche = Rouge.gauche + Rouge.largeur. La définition des méthodes dans ces contraintes est telle qu'à priorité égale, les boîtes sont déplacées plutôt que retaillées. La dernière contrainte signifie que la boîte Mauve peut se trouver n'importe où en dessous de la boîte Grise. Pour cela nous avons défini une contrainte d'inégalité entre deux variables A et B. Les méthodes associées à cette contrainte sont les suivantes :
Si B < A alors B := A, sinon rien
Si A > B alors A := B, sinon rien
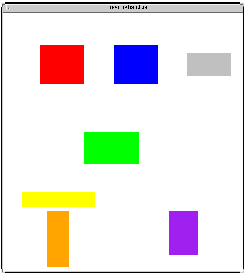
Fig 25. Interface de tests pour les résolveurs DeltaBlue et SkyBlue
[Table des matières]
8.2 Premiers retours
A partir de cette interface, nous avons fait des premiers tests avec DeltaBlue puis avec SkyBlue. Les résultats obtenus sont identiques avec les deux résolveurs, excepté pour les tests concernant la définition de contraintes cycliques.
Lors du déplacement d'un objet, les variables concernées sont mises à jour instantanément. Dans notre exemple, un mouvement vertical de la boîte Rouge entraîne un mouvement vertical identique de la boîte Bleue et inversement, mais ne déplace pas la boîte Verte qui n'est pas liée sur le même axe. Les boîtes Jaune et Orange sont centrées sur l'axe vertical, le déplacement de l'une entraîne un déplacement identique de l'autre. La modification de la largeur de l'une entraîne également un déplacement de l'autre de façon à ce que leurs axes verticaux restent confondus. Dans ce dernier cas, la résolution de la contrainte privilégie la méthode qui déplace l'objet plutôt que celle qui le retaille, conformément aux choix effectués.
L'augmentation ou la réduction de la hauteur de la boîte Bleue entraîne une modification équivalente de la hauteur de la boîte Rouge. Une modification de la largeur de la boîte Bleue n'entraîne aucune modification sur la boîte Rouge car ces deux boîtes ne possèdent pas de contraintes sur leur largeur.

Fig 26. Exemples de contraintes sur la dimension des boîtes
Un déplacement ou un agrandissement de la boîte Mauve vers le haut n'affecte pas la boîte Grise tant que cette dernière reste au dessus (Fig 27 a). Par contre, dès que le bord supérieur de la boîte Mauve atteint la valeur du bord inférieur de la boîte Grise, cette dernière suit le mouvement (Fig 27 b). De même lorsque le bord inférieur de la boîte Grise est modifié, le mouvement n'est répercuté que lorsque ce bord atteint la valeur du bord supérieur de la boîte Mauve.
La contrainte d'inégalité définie pour ce test donne des résultats attendus pour des cas simples mais s'avère plus aléatoire pour des configurations plus compliquées comme celle décrite dans la Fig 28 . Dans cet exemple, nous avons d'abord spécifié deux contraintes d'inégalité stipulant que les boîtes Rouge et Bleue ne peuvent pas sortir de la fenêtre par la gauche (leur bord gauche a une coordonnée positive). En déplaçant la boîte Rouge (a) ou la boîte Bleue (b), les contraintes sont respectées. Si on ajoute une troisième contrainte stipulant que les deux boîtes sont juxtaposées, celle-ci est prise en compte et un déplacement de la boîte Bleue entraîne un déplacement de la boîte Rouge (c). On peut déplacer la boîte Bleue jusqu'au bord gauche de la fenêtre mais la boîte Rouge en est déjà sortie (d). La contrainte d'inégalité sur la boîte Rouge n'est donc plus respectée.
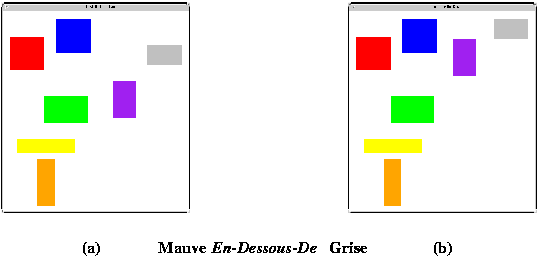
Fig 27. Exemple de contraintes d'inégalité (1)

Fig 28. Exemple de contraintes d'inégalité (2)
Nous avons ensuite testé les deux résolveurs en définissant les contraintes suivantes qui forment un cycle sur l'axe horizontal :
(1) Rouge Aligné-Haut Bleue
(2) Verte En Dessous-de(0) Rouge
(3) Verte En Dessous-de(0) Bleue
Quelles que soient les dimensions des objets, DeltaBlue n'accepte pas cette spécification, même en utilisant des contraintes de poids différents. Les cycles ne sont pas détectés avant la propagation mais lorsque celle-ci a déjà commencé. Le résolveur stoppe la propagation et envoie un message d'erreur, mais aucune image de la solution initiale n'est conservée, on ne peut donc pas revenir à la situation précédente.
SkyBlue a été testé sans résolveurs de cycles externes. Néanmoins, il accepte la spécification de ces contraintes et détecte le cycle, mais aucune action n'est effectuée. Le résultat est que SkyBlue relâche une des trois contraintes afin d'éviter le cycle, le choix de celle-ci étant fonction du poids de chacune. A poids égal, c'est la dernière contrainte considérée qui est relâchée. Dans la situation initiale, la dernière contrainte spécifiée (3) est relâchée (Fig 29 a). Par la suite, la contrainte relâchée dépend de la boîte déplacée (selon l'axe vertical). Un déplacement de la boîte Rouge est propagé à la boîte Verte (2), lui-même propagé à la boîte Bleue (3). Dans ce cas, la contrainte (1) n'est pas vérifiée (Fig 29 b). Si on déplace alors la boîte Verte, le déplacement est propagé à la boîte Bleue (3) et récursivement à la boîte Rouge (1). Cela a pour conséquence de relâcher la contrainte (2) (Fig 29 c). Ce comportement n'est pas satisfaisant pour notre problème où l'on a besoin qu'un même système de contraintes possède un comportement unique.
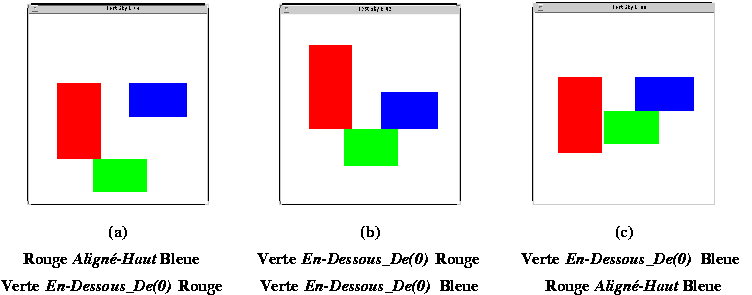
Fig 29. Exemple de contraintes cycliques avec SkyBlue
En manipulant ces prototypes, nous avons rencontré concrètement un des problèmes induits par l'utilisation de contraintes, à savoir celui de leur visualisation. En effet, même un système de contraintes simple comme celui établi pour les tests nécessite un effort de mémorisation important de la part de l'auteur. De plus, ce dernier n'a pas conscience de toutes les répercussions provoquées sur le système existant lorsqu'il ajoute ou retire une contrainte. Ce problème se pose en termes plus aigus lorsque l'utilisateur n'est pas l'auteur du système de contraintes, car il ne les découvre qu'au fur et à mesure de ses manipulations.
[Table des matières]
8.3 Sélection entre DeltaBlue et SkyBlue
D'un point de vue théorique, SkyBlue paraît plus intéressant parce qu'il est plus général que DeltaBlue. Son objectif est de combler certaines limitations de ce dernier. Cependant, à partir de l'étude théorique des deux résolveurs et des tests effectués avec le prototype précédent, nous avons choisi de retenir DeltaBlue. Ce choix repose sur le comportement de ces résolveurs en présence de cycles et sur des raisons de facilité d'utilisation, de performances et d'évolutivité.
SkyBlue n'a pas été testé avec des résolveurs de cycles externes. Sans de tels résolveurs, son comportement n'est pas satisfaisant. Néanmoins, même avec de tels résolveurs il subsiste un problème, lié à leur procédure d'appelnote3. En effet, les auteurs de l'article précisent que SkyBlue ne transmet pas toujours assez de contraintes au résolveur externe pour que celui-ci puisse trouver une solution. Dans certains cas, il est nécessaire de transmettre des contraintes ne participant pas au cycle, mais SkyBlue ne sait pas identifier lesquelles. Supposons que l'on ait le système de contraintes suivant, toutes de même poids {A=B, B=A, B=C, C=5}. La solution correcte est A=B=C=5. Si on les définit dans cet ordre, SkyBlue considère les deux premières contraintes A=B et B=A comme formant un cycle et les envoie au résolveur externe. Comme elles sont redondantes, il ne peut trouver une valeur unique pour A et B. SkyBlue marque alors ces variables comme étant incorrectes et arrête la propagation. Si SkyBlue avait envoyé toutes les contraintes au résolveur, alors celui-ci aurait pu trouver la solution. D'autres exemples de cycles non résolus à cause de ce problème sont donnés dans . La conclusion des auteurs de l'article est que SkyBlue fonctionne bien pour des applications utilisant la propagation locale et des contraintes à sorties multiples mais que pour l'utiliser avec des résolveurs externes, il doit être modifié.
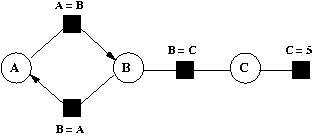
Fig 30. Exemple où la partie cyclique n'est pas suffisante pour sa résolution
Le fonctionnement de SkyBlue est plus complexe que celui de DeltaBlue et ses performances dans une situation identique sont nettement moins bonnes (sections 6.5 et 7.3), notamment parce qu'il gère des contraintes à sorties multiples. Or, ce type de contraintes n'est pas indispensable dans le cadre de Madeus. Leur utilisation éventuelle ne justifie donc pas la complexité induite.
DeltaBlue a été l'un des premiers résolveurs incrémentaux à appliquer la technique de propagation locale par valeurs et ses principes de fonctionnement servent encore aujourd'hui de référence à de nombreuses recherches dans ce domaine (, ). L'éventualité de pouvoir changer de résolveur dans Madeus pour en intégrer un plus général fait qu'il est préférable de se baser sur DeltaBlue plutôt que sur SkyBlue, lequel ne fait plus actuellement l'objet de recherches ni de développements.
Dans ce chapitre, nous avons étudié la technique de résolution de contraintes par propagation locale et son application dans des résolveurs pour des problèmes de maintien de solution. Cette étude nous a permis de mieux caractériser cette technique et de mettre en relief ses avantages et ses limitations. Elle nous a également permis de choisir l'un de ces résolveurs dans le cadre de notre projet.
[Table des matières]
9.1 Bilan sur la propagation locale
Cette technique de résolution permet de répondre au problème du maintien de solutions dans le cadre d'interfaces utilisateur interactives avec des performances très intéressantes. En contrepartie, l'approche locale utilisée par cette technique induit certaines limitations comme l'impossibilité des gérer les cycles de contraintes et les inégalités.
De nombreux travaux sur la question montrent qu'il n'existe pas de solution à ces problèmes en utilisant une approche exclusivement locale, c'est pourquoi d'autres approches ont été étudiées pour ces problèmes spécifiques.
Les études récentes dans le domaine ont abouti au développement de nouveaux résolveurs qui combinent l'approche locale et ses qualités (performance, simplicité) pour tous les cas pouvant être traités par cette approche, et l'approche globale pour les autres cas. Cette démarche est celle suivie avec le résolveur UltraViolet (section 5.1). C'est également le sens de l'étude effectuée par Gilles Trombettoni () sur la propagation locale et ses limites, ce dernier proposant des extensions à l'algorithme QuickPlan pour prendre en compte certains types de contraintes.
Néanmoins, tous ces travaux sont en phase de recherche et aucune implémentation n'est encore disponible. Une question qui se pose également avec ces résolveurs hybrides est la définition du ratio méthodes locales / méthodes globales qui est déterminant dans le gain des performances obtenues. En effet, si ce ratio tend à diminuer en faveur des méthodes globales, alors l'utilisation de résolveurs hybrides peut devenir moins pertinente et moins performante que l'utilisation d'un résolveur basé uniquement sur des approches globales.
[Table des matières]
9.2 Application à Madeus
Le choix de retenir le résolveur DeltaBlue présente plusieurs avantages. D'abord la technique de propagation locale par valeurs est une technique très performante et DeltaBlue, l'un des premiers résolveurs incrémentaux à l'utiliser, en a établi les bases. De plus DeltaBlue est relativement facile à comprendre et à utiliser. Enfin, plusieurs applications l'ont déjà utilisé ce qui montre une certaine fiabilité.
Les limitations évoquées précédemment font que DeltaBlue ne satisfaisait pas complètement les critères définis pour notre application. Dans le chapitre suivant, nous allons présenter l'extension que nous avons développée afin de pallier à la limitation concernant la définition de certaines contraintes cycliques. Nous présenterons également la mise en oeuvre du placement spatial à base de contraintes dans Madeus.
Propagate Degree Of Freedom
(2)D'après un échange de messages avec G.Oster
(3)http://www.cs.washington.edu/research/projects/weird/www/skyblue-cycles.html