Video 1 Start Texte 1
Video 1 Equal Son 1
Video 1 Before Image 1
Image 1 Start Texte 2
Image 1 Before(d3) Image 2
Texte 2 During Texte 1
Texte 2 Finish Image 2
Le scénario temporel de Madeus est défini par un ensemble de contraintes entre les objets du document. Nous allons nous intéresser dans ce chapitre à l'étude d'une visualisation graphique de ces contraintes, visualisation qui n'est pas seulement un équivalent graphique du source textuel mais qui a pour but de permettre à l'auteur d'appréhender le comportement global de son scénario.
Dans une première partie (section 2) nous présentons à la fois les besoins et les difficultés que soulève la réalisation de cette vue graphique.
Par la suite, nous présenterons une solution qui répond en partie à ces besoins. La restriction majeure que nous faisons au problème général est de considérer que les objets ont une durée unique. Par conséquent la distinction entre les objets contrôlables et les objets non-contrôlables (présentée dans la section 0.0) n'est pas prise en compte.
Cette restriction s'explique par la difficulté de manipuler dynamiquement des objets de taille variable et un placement temporel variable. L'intégration de ces deux types de contraintes nécessite l'utilisation d'un résolveur incrémental de contraintes qui permet des manipulations directes de la part de l'auteur. En effet, l'introduction de contraintes sur la durée des objets ajoutée aux contraintes de placement peuvent être à l'origine de cycles. Par exemple, lorsque l'on définit une contrainte A equal B entre deux objets de taille flexible, plusieurs contraintes sont définis dans le résolveur :
Si on trace le graphe de dépendance des variables on s'aperçoit de l'existence d'un cycle. De plus ce ce résolveur doit pouvoir gérer des contraintes d'inégalité qui traduisent des placements temporels du type A Before B.
Les travaux de L. Carcone effectués au sein du projet Opéra en parallèle à mon stage, ont permis de mettre en évidence qu'actuellement aucun résolveur ne le permettait de manière satisfaisante. Malgré cette restriction le besoin en visualisation graphique du scénario subsiste.
Nous avons porter nos efforts sur les autres aspects du problème afin de dégager et de valider des principes de base pour répondre à notre problématique initiale. Afin de diviser les problèmes nous avons choisi de traiter d'abord le problème sans structuration hiérarchique (section 3) puis d'intégrer celle-ci à la solution de base (section 4). Notre proposition fait l'objet de la réalisation d'un prototype, externe au système Madeus, qui permet à partir d'un scénario donné de visualiser l'ensemble des placements temporels possible des objets. Cette implantation a été réalisée en Tcl/Tk , un langage interprété qui nous a permis d'élaborer de manière relativement simple et rapide des prototypes d'interface.
Bien que nous n'ayons pas pu, à l'occasion de ce stage répondre à tous les besoins identifiés dans la section 2, il nous a semblé pertinent de donner dans la section 5 une première ébauche les idées que nous avons pour en traiter certains.
La section 6 est dédiée à la présentation de certains algorithmes clés utilisés pour mettre en oeuvre la solution.
La dernière partie de cette section est dédiée à la présentation des premiers tests réalisés avec des utilisateurs potentiels.
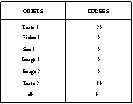
Avant de présenter les besoins et difficultés soulevés par notre la visualisation de scénario temporel, nous présentons un exemple qui servira de fil conducteur tout au long de ce chapitre. La Fig 0 donne les contraintes (la sémantique intuitive des contraintes a été présentée dans la section 0) qui relient les objets du document ainsi que la durée des objets. Tous les objets considérés ici sont des objets de base (pas de structure hiérarchique).
|
Video 1 Start Texte 1 Video 1 Equal Son 1 Video 1 Before Image 1 Image 1 Start Texte 2 Image 1 Before(d3) Image 2 Texte 2 During Texte 1 Texte 2 Finish Image 2 |
|
Fig 0. Le scénario de référence
Dans la Fig 1 nous montrons un placement temporel possible des objets.
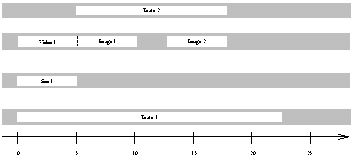
Fig 1. Un exemple de placement temporel
Nous allons maintenant présenter les différents besoins liés à la visualisation graphique du scénario temporel (le problème est traité ici sans restriction).
Une des idées fortes de l'approche adoptée dans Madeus est que l'auteur n'a pas à fixer la durée précise de chaque objet. C'est au système de calculer l'ensemble des durées de manière à satisfaire la spécification (rôle du planificateur ou formateur temporel). Pour cela, deux types d'objets sont différenciés dans Madeus : les objets contrôlables et les objets non-contrôlables (qui ont été introduits dans la section 0).
Par conséquent, non seulement la durée des objets que l'on manipule n'est pas unique, elle varie dans un intervalle délimité par des bornes, mais en plus ces intervalles de durées possibles ont deux sémantiques différentes pour l'auteur. Dans le cas des objets contrôlables, c'est un intervalle de choix et l'auteur peut, s'il le souhaite, changer sa valeur en modifiant sa spécification. Dans le cas des objets incontrôlables, c'est un intervalle de valeurs possibles à l'exécution sur lequel l'auteur ne peut rien faire. Il est donc nécessaire de faire apparaître cette différence lors de la visualisation.
Certaines relations de placement relatif introduisent la présence de délai "flexible". C'est le cas par exemple des relations Before ou During. Le délai entre les deux objets n'est pas fixé, c'est un délai contrôlable au sens défini ci-dessus.
La nature des objets ainsi que celle des relations conduisent à la visualisation d'un ensemble de solutions et non pas d'une solution unique, ce qui rend plus complexe le problème auquel nous tentons d'apporter une solution.
Etant donnée une spécification, certaines configurations de placement des objets dans le temps sont possibles alors que d'autres ne le sont pas. Comprendre les raisons de ce partage est une tâche complexe, car la cause peut provenir d'une contrainte induite par transitivité à partir des contraintes placées par l'auteur. Nous donnons ici un exemple de contrainte induite : si l'auteur spécifie "A Before B' et "B Before C", on obtient une contrainte induite qui est "A Before C".
On rejoint avec ce souci de visualiser les causes d'une configuration la volonté de satisfaire le critère d'observabilité tel qu'il est défini dans la section 0. Nous avons vu dans la section 0 avec Microsoft Project que ce besoin est ressenti dès que l'on utilise des contraintes.
Si l'on considère l'exemple donné en introduction, il n'est pas possible de rapprocher Image 2 de Video 1 en deçà d'une certaine limite à cause des contraintes placées entre Image 2 et Image 1 (Image 1 before(d3) Image 2) d'une part, et entre Image 1 et Video 1 (Video 1 before Image 1) d'autre part.
Il faut donc trouver un moyen efficace pour aider l'auteur dans cette tâche de compréhension. Cela pose le problème de visualisation des contraintes. Doit-on les représenter explicitement au risque de surcharger l'affichage, comme dans le système FireFly présenté dans la section 0.0, et dans ce cas comment traitons-nous les contraintes induites par transitivité ?
Cette aide est d'autant plus difficile à mettre en place qu'une même configuration d'objets peut être obtenue par des spécifications différentes et qu'il est important pour l'auteur de visualiser ces différences. En effet, deux placements identiques mais s'interprétant de manière différente, peuvent mener à des ensembles de configurations différentes. Par exemple, la configuration présentée dans la Fig 1 peut aussi s'obtenir en remplaçant la contrainte Vidéo 1 equal Son 1 par Son 1 Before Image 1. Dans les deux cas, nous obtenons un ensemble de solutions différent, même s'ils ont des solutions communes.
Pour faciliter la compréhension de cette section, nous allons étendre l'exemple introductif (section 1) pour intégrer la notion de hiérarchie. Nous utilisons une hiérarchie simple définie avec trois objets composites :
Les éléments des scènes 1 et 2 sont représentés dans la Fig 2 . Les contraintes définies entre les objets de ces deux scènes sont celles introduites dans l'exemple introductif (Fig 0 ).
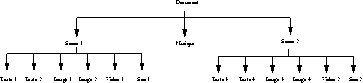
Fig 2. Un exemple de hiérarchie
Les relations entre les objets Scène 1, Scène 2 et Musique sont définies dans la Fig 3 .
Scène 1 Equal Scène 2
Scène 1 Equal Musique
Fig 3. Extension de l'exemple de la Fig 0
Dans Madeus, il est possible de décomposer hiérarchiquement son document afin de maîtriser sa complexité. Cette hiérarchie se retrouve au niveau de la spécification temporelle du document. Plus précisément, à chaque objet composite de la hiérarchie est associé un ensemble de contraintes temporelles reliant potentiellement tous les fils de cet objet. Autrement dit, tous les fils d'un même père forment un groupe et sont reliés par des contraintes temporelles. Si l'on considère l'exemple de la Fig 2 , des contraintes peuvent relier les scènes 1, 2 et l'objet Musique. Un autre ensemble de contraintes relie les objets composant la Scène 1 et ainsi de suite. Par conséquent, la structure hiérarchique n'est pas complètement déconnectée de la visualisation des placements temporels et il paraît important de pouvoir visualiser ces deux informations au sein d'un même affichage. Dans l'exemple de la Fig 2 , il est nécessaire que l'auteur puisse visualiser dans une même vue les composants de la Scène 2 et ceux de la Scène 1, même s'ils n'ont pas de liens directs entre eux, car la contrainte mise sur les objets Scène 1 et Scène 2 impose un recouvrement temporel entre leurs composants. L'auteur doit aussi pouvoir visualiser s'il le souhaite, le contenu de deux scènes mises en séquence pour voir comment s'effectue leur transition.
L'auteur a donc besoin de :
Nous voulons mettre ici en évidence le problème de la représentation à l'échelle de la durée des objets et de la visualisation du document dans sa globalité. Les difficultés qui se posent ici sont classiques et sont liées aux limitations physiques de la taille d'un écran et des capacités de perception humaines.
Imaginons par exemple, que l'objet Texte 1 (qui par exemple peut être le titre de la présentation) soit présent tout au long du document et dure 25 minutes, et qu'à un moment de sa présentation nous affichions une image qui reste 5 secondes à l'écran. Si nous affichons dans la vue graphique du scénario des objets dont la longueur est proportionnelle à leur durée, il faut que la taille de Texte 1 soit environ deux cent fois plus grande que la taille de l'image. Il n'est donc pas possible de visualiser complètement les deux objets à l'échelle tout en voulant que l'objet Image 1 reste preceptible.
Parmi l'ensemble des configurations possibles que peuvent avoir deux objets, certaines sont plus "chargées d'informations" que d'autres. Par exemple, placer deux objets A et B de manière à ce qu'ils démarrent en même temps alors que cette configuration particulière n'est pas requise par les contraintes est un choix malencontreux qu'il faut éviter. On rejoint ici la volonté de satisfaire le critère d'honnêteté tel que défini dans .
Dans l'exemple introductif (section 1), le placement temporel que nous avons choisi de montrer pour illustrer l'exemple est tel que les objets Video 1 et Image 1 se touchent, pourtant aucune contrainte ne force ce placement, mais aucune ne l'interdit. Nous souhaitons proposer une visualisation qui évite autant que possible ce genre de configuration et donc l'interprétation erronée du scénario temporel.
Remarquons ici, comme nous l'avions observé dans la section 0.0 que la solution de visualisation proposée dans l'environnement ISIS ne satisfait pas ce besoin.
L'introduction d'une vue graphique du scénario introduit une troisième vue au sein de Madeus (vue d'édition textuelle, vue graphique du scénario, vue d'exécution du document (Fig 0 )).
Il est donc nécessaire de permettre à l'auteur de faire aisément le lien entre ces trois vues.
Dans l'exemple introductif, nous voyons que la donnée d'un exemple de placement (Fig 1 ) temporel ne permet pas à l'auteur de visualiser les contraintes spécifiées. On retrouve ici le besoin de visualiser les contraintes exprimées par l'auteur déjà évoqué dans la section 2.2.
Le premier besoin ressenti concerne la liaison entre la vue graphique du scénario temporel et la fenêtre comportant le source textuel. Ce lien doit d'être à double sens. En effet, quand l'auteur sélectionne une contrainte dans le source textuel, il doit pouvoir visualiser l'impact qu'elle a dans la vue graphique du scénario. De plus, quand il sélectionne un objet il doit pouvoir visualiser l'ensemble des contraintes directes qui sont sur cet objet.
De manière symétrique il est nécessaire de faire le lien entre la vue graphique du scénario temporel et la fenêtre d'exécution. Comme dans le cas précédent ce lien doit être à double sens. En effet, lorsque l'auteur joue le scénario il doit pouvoir visualiser à quel endroit il se trouve dans la vue graphique du scénario temporel. De même, quand il manipule la vue graphique et qu'il se place à un instant précis à l'intérieur, il doit pouvoir visualiser "un instantané" de la fenêtre d'exécution, par exemple pour avoir des informations sur le placement spatial des objets.
Un autre besoin que nous avons identifié est la visualisation de la structure de navigation. Les objets de Madeus peuvent être associés à des liens potentiellement activables (les différents types de liens ont été présentés dans la section 0). Le problème consiste donc à visualiser statiquement ces possibilités offertes au lecteur.
Dans l'exemple introductif, si nous ajoutions un lien de type inclusion à l'objet Texte 1, de telle façon que lorsqu'on clique dessus un objet composite soit joué en même temps, il faut permettre à l'auteur de le visualiser dans la vue graphique du scénario temporel.
Une autre difficulté est le problème du passage à l'échelle. En effet, une méthode de visualisation qui s'avère bonne pour de petits documents peut s'avérer difficilement compréhensible pour de gros documents (qui peuvent comporter des centaines d'objets). Le problème sera donc de trouver une méthode de visualisation qui soit adaptée pour tous les documents. On a vu que les systèmes actuels répondaient mal à ce critère.
Il est nécessaire de bien distinguer l'opérateur parmin de l'opérateur equal. En effet, les deux opérateurs se traduisent par un placement temporel identique : les opérandes démarrent en même temps et se terminent en même temps mais leur sémantique est différente: dans le cas du parmin, il se peut que l'un des deux opérandes ait été interrompu. Cette différence doit apparaître dans la vue graphique du scénario. De plus il est important pour l'auteur de savoir précisément quels sont les objets qui risquent d'être interrompus, car ceux-ci peuvent potentiellement ne pas délivrer la totalité de leur contenu.
Cette information n'est pas simple à connaître dès que les objets manipulés peuvent avoir différentes durées et que de plus il existe des objets incontrôlables. Considérons par exemple une relation A parmin B où A est un objet contrôlable dans l'intervalle [10, 15] et B est un objet incontrôlable dans l'intervalle [8, 12]. Parmi l'ensemble des exécutions possibles, certaines interrompent A (par exemple si A=10 et B=8), d'autres interrompent B (par exemple si A=10 et B=12). Cependant, l'auteur, qui peut agir sur la durée de A, peut modifier son intervalle de valeurs possibles pour qu'il ne soit jamais interrompu (par exemple en le fixant à [12, 15]). Il ne peut pas faire de même avec B car celui ci est incontrôlable. Ce sont toutes ces informations qu'il faut pouvoir fournir à l'auteur. Le problème est tout aussi difficile avec l'autre opérateur d'interruption (le parmaster) qui se traduit selon les cas soit par une interruption soit par le déroulement complet des deux objets.
Nous concluons cette partie analyse des besoins en précisant les points que nous avons abordés au cours du stage. Les autres sont évoqués dans la partie perspective qui termine ce chapitre. Sous l'hypothèse de durée unique des objets, nous avons apporté une réponse aux besoins suivants :
Les trois premiers points sont présentés dans la section 3, et la visualisation de la hiérarchie sera traitée dans la section 4.
L'idée générale sur laquelle repose notre proposition est la suivante : nous proposons à l'auteur un placement possible des objets sur un ensemble d'axes temporels et nous matérialisons sur cette vue toutes les contraintes présentes dans le scénario. L'auteur peut manipuler (en déplaçant les objets sur leur axe temporel) cette vue afin de parcourir l'ensemble des placements temporels possibles à partir du scénario.
Nous commençons par présenter comment nous visualisons les objets, puis comment sont visualisées les contraintes exprimées dans le scénario (section 3.1). Dans une deuxième partie (section 3.2) nous présentons comment l'auteur visualise l'ensemble des solutions possibles à partir du scénario. Dans une troisième partie nous expliquons le lien entre les différentes fenêtres.
Les objets de base sont représentés par des rectangles dont la longueur est proportionnelle à leur durée effective. Chaque type d'objet (vidéo, son, texte, image) est représenté par un motif discriminant (voir Fig 4 ). Les objets sont placés sur des lignes horizontales qui représentent des axes temporels, le temps s'écoulant de gauche à droite. Les lignes donnent aussi l'intuition du déplacement temporel par un déplacement graphique horizontal des objets.
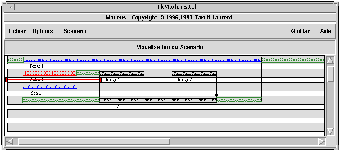
Fig 4. Vue graphique du scénario donné en exemple
Hormis les objets, les contraintes introduisent deux types d'éléments dans la vue graphique :
La représentation explicite des objets, des contraintes et des délais introduits par ces contraintes permet une interprétation directe du scénario sans nécessairement avoir recours à la vue textuelle. Cela permet d'envisager la disparition de la vue textuelle telle qu'elle est actuellement dans Madeus, le jour où l'édition du scénario temporel se fera dans la vue graphique du scénario.
Lorsqu'on sélectionne et déplace un objet, tous les objets dont le placement temporel est solidaire à cet objet (ils lui sont reliés par des contraintes qui n'introduisent pas de délais flexibles) suivent les mouvements imposés par l'objet sélectionné. Lors de cette sélection, l'objet sélectionné apparaît en rouge et les objets qui lui sont solidaires apparaissent en bleu. En vert apparaissent tous les délais flexibles dont la valeur est susceptible d'être modifiée par des déplacements de l'objet sélectionné.
Afin d'aider l'auteur dans le parcours de l'ensemble des solutions nous avons jugé opportun de lui fournir la visualisation de l'intervalle de déplacement de manière à ce qu'il puisse anticiper le comportement de l'objet qu'il manipule (critère de prévisibilité). On retrouve ici l'idée des axes de déplacement possibles visualisés dans Drawing with Constraint (section 0.0).
Dans l'exemple de la Fig 5 , l'auteur a sélectionné l'objet Texte 2. Un trait rouge apparaît sous la ligne où est placé l'objet sélectionné, indiquant ainsi la latitude de déplacement de l'objet dans les deux sens. Sur notre exemple, Texte 2 est limité à sa gauche par la fin de l'objet Vidéo 1 et est limité à sa droite par la fin de l'objet Texte 1.
Fig 5. Visualisation d'informations
Ce choix de ne visualiser des informations pertinentes que lorsque l'auteur sélectionne un objet nous semble primordial pour éviter de surcharger la fenêtre et pour limiter l'effort cognitif nécessaire à la compréhension de cette dernière.
Dans cette solution, nous avons fait le choix de ne pas bouger les objets qui ne sont pas liés par des contraintes rigides (qui n'introduisent pas de délais flexibles) avec l'objet sélectionné. Un autre choix aurait été de bouger tous les objets liés avec l'objet sélectionné. L'idée de cette autre solution est la suivante : l'objet sélectionné après avoir absorbé un délai flexible ne se bloque plus sur l'objet atteint mais l'entraîne avec lui dans son déplacement.
Pratiquement cela revenait à tout bouger. Nous avons pensé que cela demanderait un effort cognitif trop important à l'auteur pour appréhender le comportement global d'un déplacement. Néanmoins tous les placements possibles restent accessibles à l'auteur. Pour cela, il lui suffit simplement de sélectionner un autre objet.
Sur l'exemple de la Fig 5 , si nous voulons déplacer Image 1 jusqu'à la fin de Video 1, il aurait fallu déplacer Video 1, mais aussi Son 1 et Texte 1, et donc tous les objets de la scène. Cela aurait été gênant pour l'auteur, car trop complexe. Si l'auteur veut atteindre une telle position il lui faut sélectionner Image 1 et le déplacer jusqu'à la position voulue, puis redéplacer Video 1.
Bien évidemment, lorsque l'auteur déplace un objet sur le time-line, la solution courante du scénario ainsi que la représentation graphique de cette dernière évolue immédiatement de manière à s'adapter aux modifications que l'on a faites (ie: la position des objets et des intervalles s'adapte et est visualisée mmédiatement à l'écran). Par exemple, la Fig 6 montre la vue obtenue lorsqu'on déplace l'objet Texte 2 le plus à droite possible.
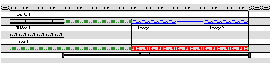
Fig 6. Texte 2 le plus à droite possible
Comme nous l'avons dit dans la section 2.6 il est nécessaire de faire explicitement le lien entre les différentes fenêtres. Dans cette solutio, nous nous sommes intéressés à deux types de lien:
Dans le premier cas (Fig 7 ), lorsque l'auteur sélectionne une contrainte dans la vue textuelle du scénario temporel, on visualise dans la vue graphique les objets et les délais introduits par cette contrainte. Dans l'exemple de la Fig 7 , l'auteur sélectionne une contrainte, tous les objets avec lesquels elle est directement liée sont mis en évidence.
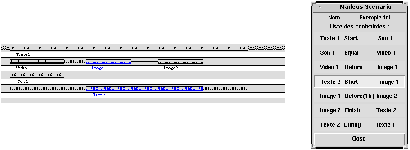
Fig 7. Liens entre les vues textuelle et graphique du scénario
Dans le second cas, lorsque l'auteur sélectionne un délai (fixe ou flexible) dans la vue graphique (Fig 9 ), il visualise dans la vue textuelle la contrainte à l'origine de cet intervalle. Lorsqu'il sélectionne un objet dans la vue graphique (Fig 8 ), il peut visualiser l'ensemble des contraintes liées à cet objet.
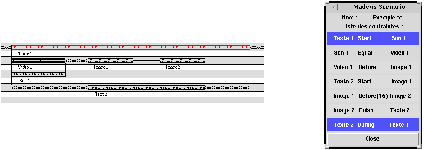
Fig 8. Liens entre les vues graphique et textuelle du scénario (a)
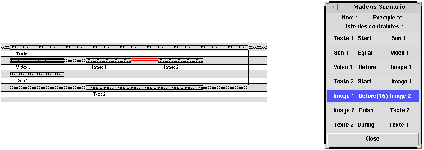
Fig 9. Liens entre les vues graphique et textuelle du scénario (b)
La visualisation des causes d'une configuration se ramène dans notre cas à visualiser les causes qui limitent le déplacement d'un objet. En effet, la visualisation du "qui" bloque le déplacement de l'objet et du "où" il se bloque ne suffise pas, il faut aussi le "pourquoi" il se bloque. Un objet se bloque que si un des délais flexibles liés à son déplacement (ressort vert) devient nul. Cette information est donnée dans notre vue et de plus, grâce au mécanisme de liaison entre la fenêtre source et la vue textuelle, il est facile pour l'auteur de comprendre d'où vient ce délai flexible.
Sur l'exemple de la figure Fig 10 il faut visualiser le fait que l'objet Image 1 est bloqué dans son déplacement à droite par l'objet Texte 1 à cause des relations Image 1 Start Texte 2 et Texte 2 During Texte 1.
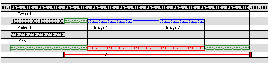
Fig 10. Visualisation d'informations
La solution que nous venons de présenter visualise un niveau de contraintes entre les objets. Nous présentons à présent la manière d'intégrer différents niveaux de hiérarchie à cette vue. Nous rappelons que des contraintes peuvent être placées entre deux objets si et seulement si ils partagent le même père.
Rappelons aussi que l'auteur a besoin non seulement de visualiser l'ensemble des placements possibles des objets reliés par le même père (ils font partie d'un même groupe), mais aussi de voir simultanément le placement d'objets qui ne font pas partie du même groupe pour, par exemple, affiner la transition entre deux scènes en séquence. C'est ce dernier cas qui rend complexe le problème d'intégration de la hiérarchie, puisque dans le premier cas toute méthode "classique" (arbre, structure indentée) ou plus novatrice (arbre conique) de représentation de la hiérarchie est satisfaisante. Il aurait en effet suffit d'associer à chacun des pères la vue graphique du scénario définie précédemment et de donner la possibilité à l'auteur d'ouvrir et fermer ces vues en cliquant sur les noeuds pères.
Dans l'article une première solution de visualisation pour représenter dans une même vue la structure hiérarchique et les informations temporelles au sein de Madeus a été présentée (Fig 11 ). Cependant, les informations temporelles sont uniquement constituées par le nom des contraintes qui relient les objets fils d'un même père. La sémantique de ces contraintes n'est donc pas visualisée.
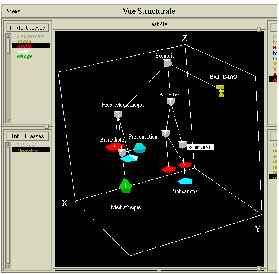
Fig 11. Visualisation de la hiérarhie
Afin de satisfaire les trois types de besoins énoncés dans la section 2.3, nous avons opté pour un affichage de la hiérarchie à l'intérieur du scénario temporel (solution inspirée de Microsoft Project (section 0)) associé à une vue de la hiérarchie sans informations temporelles.
Sur la Fig 12 nous voyons la fenêtre de visualisation associée à notre exemple avec à gauche le premier niveau de hiérarchie et à droite la vue graphique associée à l'ensemble des contraintes qui relient ces trois objets. L'auteur peut ouvrir ou fermer un niveau de hiérarchie en cliquant dessus (Fig 13 ).

Fig 12. Hiérarchie fermée
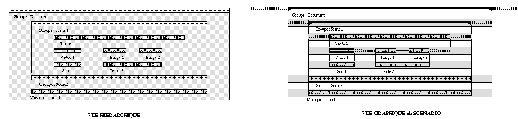
Fig 13. Hiérarchie ouverte
Une fois ouvert, l'objet composite reste visible dans la vue graphique du scénario et peut être soumis à des déplacements. Dans ce cas, nous appliquons le principe suivant : tous les objets du même niveau qui ont une relation forte avec cet objet sont mis en bleu, ainsi que tous leurs descendants. Tous les objets suivent les déplacements de l'objet sélectionné. Les rails de déplacement que nous visualisons à chaque niveau limitent les déplacements de l'objet à son niveau de hiérarchie. Par exemple lorsque l'élément Musique de fond est sélectionné il ne peut se déplacer qu'entre le début et la fin de son père (le groupe Document (Fig 14 )).
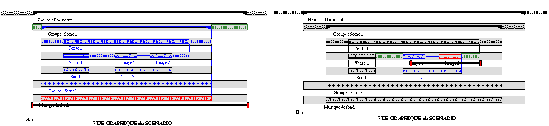
Fig 14. Sélection d'éléments
Nous avons choisi de représenter explicitement la hiérarchie de manière à offrir à l'utilisateur une vue directe et aisément compréhensible de cette dernière, avec la possibilité de faire des manipulations directes (ouvrir, fermer des objets composites) dessus sans avoir toutes les informations temporelles associées aux objets. Une de nos premières idées avait été de représenter cette hiérarchie sous la forme d'un arbre n-aire. Cependant la difficulté était de faire directement le lien entre la vue hiérarchique et la vue graphique du scénario temporel. Par conséquent, afin de faciliter ce problème de liaison entre les vues, nous avons imaginé une vue hiérarchique qui de part le placement spatial des objets reste très proche de la vue du scénario.
Nous présentons ici les idées que nous avons pour aborder certains des points qui ont été soulevés dans la partie besoin et pour lesquelles nous n'avons pas eu le temps d'apporter une réponse complète. Nous nous plaçons encore ici sous l'hypothèse de durée unique des objets.
Fig 15. Visualisation des opérateurs d'interruptions
Fig 16. Exemple de liens
Nous avons vu qu'il y avait deux aspects :
Dans le premier cas (Fig 17 ), ce lien est réalisé au moyen d'une ligne temporelle, qui permet de définir "un instant" dans le scénario temporel, et de placer cet instant dans la fenêtre où nous visualisons l'exécution du scénario. Cela permet d'avoir un "instantané" du scénario.
Fig 17. Liens entre la vue graphique et l'exécution du scénario
Fig 18. Problème du lien
Fig 19. Problème du lien
Pour mettre en oeuvre notre solution il nous a fallu résoudre les problèmes suivants :
Pour cela nous nous sommes appuyés sur la structure de graphe d'instants qui est construite par le système Madeus à partir du source textuel. Nous présentons brièvement cette structure, sa construction et la structure de données qui lui est associée dans nos algorithmes (section 6.1). Nous présentons ensuite séparément les algorithmes utilisés pour répondre à chacun des deux points précédemment évoqués (section 6.2 et section 6.3). Nous rappelons que ces algorithmes ont fait l'objet d'une implémentation en Tcl/Tk. L'outil de développement d'interface Tcl/Tk est constitué d'un langage de programmation, Tcl (Tool Command Langage), qui est associé à une boite à outils X windows (Tk).
Le problème du choix des objets à placer sur le même axe temporel en étant certain que ceux-ci ne se recouvreront jamais quelques soient les déplacements effectués par l'auteur se règle facilement en s'aidant du graphe temporel.
Une difficulté que nous n'évoquons pas ici car nous ne l'avons pas traitée est le calcul du bon placement initial des objets sur les lignes (axes temporels) de manière à éviter les coupures des objets ou délais par des traits verticaux.
Le graphe temporel est un graphe acyclique orienté, dont les noeuds sont les instants de début et de fin des intervalles et dont les arcs représentent la durée.
Pour expliquer la construction du graphe temporel (pour plus de détails voir ) nous allons donner l'idée de la construction incrémentale de ce graphe.
Nous distinguons deux types d'actions :
L'objet est représenté pas un intervalle. Nous créerons donc un arc entre deux noeuds.
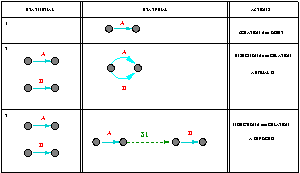
Fig 20. Construction du graphe temporel
L'insertion d'une relation entre deux objets a pour effet de modifier le graphe temporel. Ces modifications peuvent être de deux types:
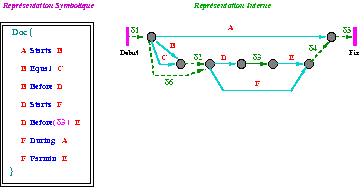
Fig 21. Le graphe temporel interne
Dans la Fig 21 nous présentons le graphe temporel associé à notre exemple introductif (1). Dans le cas général (objets contrôlables et non contrôlables) les arcs sont paramétrés par un triplé de valeurs qui représentent les durées minimale, maximale et optimale.
Nous allons décrire maintenant rapidement la structure de données utilisée;
# Définition des types propres à la manipulation des graphes temporels
Type T_Arc # un arc relie deux noeuds
Noeud1, Noeud2 : T_Noeud Objet : T_Objet
Type T_Noeud # un noeud est le point de départ d'une liste d'arcs, # Les arcs sont orientés dans la SDD (structure de données) en fonction du placement # temporel des objets
L_arc : Liste( T_Arc)
Type T_Objet # Les objets ont des informations qui leurs sont # propres: # - Durées (min,max, idéale, réelle) # - Position # et un lien vers l'arc auquel ils sont associés
Durees : T_Info Position : T_Info Arc : T_Arc
Type T_Hiérarchie # La structure T_Hiérarchie permet de manipuler les informations # sur les éléments de la hiérarchie. Plusieurs informations sont sauvées : # - les fils du niveau # - les positionsabsolues (qui seront mises à jour par lesystème) et relatives du niveau #
Xrel, YRel : T_Info # Les positions relatives Xabs, Yabs : T_info # les positions absolues
# Nous allons utilisé par la suite différentes fonctions que nous ne détaillerons pas :
Liste_arc : qui à partir d'un noeud renvoie la liste d'arc associés à ce noeud.
Type : permet de savoir le type de l'objet, c'est-à-dire si c'est un intervalle flexible ou pas.
Marque_Existe : qui nous dit si un noeud est marqué.
Marque : Marque un noeud.
Objet_Associer : renvoie l'objet associé à un intervalle.
Arc_Associer : renvoie l'arc associer à deux noeuds.
Orientation : nous permet de savoir si nous parcourons l'arc dans le sens du temps.
Initialisation_varialbes_locales : met à jour toutes les variables locales nécessaires.
DeplacementPermis : permet de savoir si l'auteur veut déplacer l'objet sélectionné
dans une zone autorisée.
CorrectionNecessaire : permet de savoir si une correction est nécessaire.
# nous expliquons par la suite dans quel cas nous avons besoin d'effectuer une correction.
# Pour toutes les fonctions de mise à jour de variables, nous nous sonmes permis
# quelques libertés, comme l'utilisation d'une fonction unique Mise_A_jours
# qui permet d'effectuer ces mises à jours.
# La procédure Calcul_structure_déplacement est le coeur du noyau
# fonctionnel du programme. Elle permet, à partir d'un objet selectionné de
# calculer tous les objets qui vont se déplacer, ainsi que les intervalles
# qui vont évoluer au cours des déplacements.
# La liste des objets qui vont se déplacer est sauvegardée dans la variable : Liste_Qui_Bouge
# Les délais qui amortissent les déplacements sont sauvés dans deux listes.
# Ce choix s'explique par le fait que certains objets vont s'allonger et d'autre
# rétrécir lorsque l'objet sélectionner va se déplacer. Le comportement des
# objets est lié au sens de déplacement de l'objet sélectionné. En effet, lorsque
# ce sens s'inverse le comportement des délais s'inverse aussi.
# Les délais qui amortissent sont donc sauvegarder dans deux listes :
# - Liste_Amortie _Droite , pour les délais qui vont rétrécir
# quand l'objet sélectionner va se déplacer à droite, et s'allonger quand il se
# déplacer à gauche
# - Liste_Amortie _Gauche, pour les objets qui délais qui vont rétrécir
# quand l'objet sélectionner va se déplacer à gauche.
# Les objet qui bloque le déplacement sont sauvés dans deux listes:
# - ListeBloqueD (droite)
# - ListeBloqueG (gauche)
Procedure Calcul_structure_deplacement
# Définition des paramètres
in => Ob : T_Objet
G : T_Graphe temporel
out =>
# Définition des variables locales
Soient :
Noeud1 := Premier_Noeud (Inter)
Noeud2 := Second_Noeud(Inter)
DébutProc Pourchaque Elmt de Liste_Arc(Noeud1) faire # On parcourt tous les arcs qui partent du # noeud1 # On insert des marques pour éviter de # boucler dans le graphe Si MarqueExiste(Elmt)faire Sortir_de_cette_iteration # On passe à l'élément suivant Sinon faire Marquer(Elmt) FinSi Selon Type(Elmt) cas DelaiVariable faire: Soit tmp := Objet_Associer(Noeud,Elmt) arc := Arc_Associer(Elmt,tmp) Selon Orientation(arc) cas Elmt -> tmp faire : # Le delai va évoluer au cours # du déplacement, on l'insert # donc dans la liste AmortieG Met_a_Jour(L_AmortieG,tmp) # Le delai, s'il est le # plus petit des delais, # sera le delai bloquant,on # met cette information a jour. Met_a_jour(DeltaXg,tmp) # On rajoute le délai dans la # liste des délais qui évoluent. Soit: tmp:=Objet_Associer(Noeud,Elmt) Met_a_jour(L_BloqueG,tmp) cas tmp -> Elmt faire : # Le délai va évoluer au cours # du déplacement, on l'insert # donc dans la liste AmortieD Met_a_Jour(L_AmortieD,tmp) # Le délai, s'il est le # plus petit des délais, # sera le délai bloquant,on # met cette information à jour. Met_a_jour(DeltaXd,tmp) # On rajoute le délai dans la # liste des délais qui évoluent. Soit: tmp:=Objet_Associer(Noeud,Elmt) Met_a_jour(L_Bloqued,tmp) FinSelon cas Video, Son, Image, Texte, DelaiFixe faire : Soit : tmp := Objet_Associer(Noeud,Elmt) # Dans le cas ou on a un objet qqc, # cet objet suivra le déplacement # on le rajoute donc dans la liste Met_A_Jour(Liste_Qui_Bouge,tmp) Calcul_structure_deplacement(tmp,G) FinSelon FinPourChaque # on traite de façon relativement similaire le # deuxième noeud FinProc
# Quand on sélectionne un objet, on calcule la structure de déplacement
# cette structure ne sera plus calculée au cours du déplacement
# elle sera mise à jour à la fin du déplacement
Procedure Debut_deplacement
in => Ob : T_Objet
G : T_Graphe temporel
out =>
DebutProc
Calcul_structure_deplacement(Ob,G)
FinProc
# La fonction déplacement sera appelée à chaque traitement du
# mouvement de la souris. L'information récupérée sur le déplacement de
# la souris n'est pas livrée (donc traitée) en continu.
# La fonction fera les corrections nécessaires et mettra à jour
# l'affichage graphique. Des corrections sont dues à la discontinuité dans
# le traitement des mouvements de la souris.
# Prenons par exemple le cas de deux objets A et B, reliés par
# un " A before B", placés sur la même ligne et supposons que nous déplaçons
# B vers A. Il se peut qu'entre deux traitements de la souris, la souris ait
# atteint une position invalide. Dans ce cas, il ne faut pas que l'objet
# suive la souris, ni qu'il reste à la dernière position valide connue. Il faut
# qu'il se "replace" depuis la dernière position connue jusqu'à la
# dernière position valide parcourue par la souris.
# Lorsque l'objet ne peut plus se déplacer, il est "bloqué".
Procedure Deplacement
in => Ob : T_Objet
Delta : T_Intervalle
out =>
DebutProc
Si DeplacementPermis(Delta)faire
Si CorrectionNecessaire(Delta)
FaireCorrection ;
FinSi
# on met à jours les objets dont la taille ou la position a
# évoluée.
Met_a_Jour(Affichage)
FinSi
FinProc
# A la fin du deplacement nous mettons à jours la SDD
Procedure Fin_deplacement
in => Ob : T_Objet
G : T_Graphe temporel
out =>
DebutProc
Mettre_A_Jour(SDD,Xoriginal,DeltaX)
FinProc
# La procédure Calcul_Position_relative permet de mettre à jour la SDD. Elle calcule la
# position absolue des objets affichés en fonction des niveaux de hiérarchie ouverts.
Procedure Calcul_Position_Relative
in => Niveau : T_Hierarchie out => DebutProc Initialisation_Variables_Locales Si Type(Niveau) = Elementaire # Nous sommes dans le cas où nous pointons sur un objet # élémentaire,toutes les variables globales ont été # mises à jour au niveau supérieur, il suffit donc de # mettre à jour la position en fonction de la # position relative de l'objet (en X) et de son décalage # (en X et en Y). Mettre_A_Jour(SDD,Niveau.Xr,Xabs) Mettre_A_Jour(SDD,Niveau.Yr,Yabs) Sinon # Type(Niveau) = Complexe Si Etat(Niveau) = Fermé # Nous sommes dans le cas ou nous sommes sur un # un niveau de hiérarchie ferme. # Toutes les variables globales ont été mises à jour # au niveau supérieur, il suffit donc de mettre a # jours la position en fonction de la position # relative de l'objet (en X) et de son décalage # (en X et en Y). Mettre_A_Jour(SDD,Niveau.Xr,Xabs) Mettre_A_Jour(SDD,Niveau.Yr,Yabs) Sinon /* Etat(Niveau) = Ouvert */ # Nous sommes dans le cas ou nous sommes sur un # un niveau de hiérarchie ouvert. # Il faut calculer les informations dans tous les # niveaux inférieurs et répercuter les informations # nécessaires à la suite du traitement # Il faut aussi mettre à jours les informations sur # le noeud courant. # Mise à jour des informations locales Mettre_A_Jour(SDD,Niveau.Xr,Xabs) Mettre_A_Jour(SDD,Niveau.Yr,Yabs) # On effectue un tri des fils du noeud courant # selon un ordre spécifique. # Dans un premier temps on les classe par ligne # et dans un second temps, à l`intérieur de ces # lignes, on les classe dans l'ordre croissant # de leur apparition (dans le temps). # Le fait de manipuler une solution et # un découpage en lignes fait que cet ordre # est total à l'intérieur d'un niveau de # la hiérarchie. Tri_des_Fils_Ligne_Placement_Temporel (Niveau) # On effectue une sauvegarde de la valeur du # Y globale de manière à pouvoir la passer # au frère du niveau courant pour la suite # du traitement. Sauvegarde(Xabs,Yabs) # Met a jours le Xglobal pour les fils en # fonction de la position du père. Mettre_A_Jour(SDD,Xabs,Niveau.Xr) # on effectue le traitement pour chaque fils, # en fonction de l'odre calculé précédemment. Pourchaque fils de Niveau faire Sauvegarde(Xabs) Mettre_A_Jour(SDD,Xabs,Niveau.Xr) # Si l'objet est le premier d'une ligne on # incremente le Y global Si PremierLigne( fils) Mettre_A_Jour(SDD,Yabs) Fin Si # sauvegarde le Y global pour les freres # du fils Sauvegarde(Yabs) # Calcul recursif du placement ResLoc := Calculer_Position_Relative (fils) # On sauvegarde la valeur de la ligne # la plus basse du niveau courant, # pour pouvoir dessiner une # boite englobante ResAbs := Maximum (ResAbs, ResLoc) # on restaure les valeurs de X et Y pour # la suite du niveau. Restaurer(Xabs) Restaurer(Yabs) Fin PourChaque # On restaure les valeurs pour le traitement # des frères du niveau courant Restaurer(Xabs) Mettre_A_Jours(SDD, DerniereLigne, ResAbs) Mettre_A_Jours(SDD,Yabs,ResAbs) Fin Si Fin Si FinProc
La réalisation de ce prototype a permis d'effectuer un début d'évaluation. Dans la mesure où l'évaluation n'a pas été effectuée avec toutes les règles requises il faut considérer les résultats qui suivent comme des premières indications. Le but était d'évaluer notre interface de visualisation du scénario temporel dont l'objectif est d'aider l'auteur à appréhender le comportement du scénario temporel. Pour cela nous avons réalisé des sessions de tests. Nous avons demandé à différentes personnes (une dizaine), de profil différent, d'utiliser notre prototype. Après une brève description de ce qu'était un scénario temporel, nous leur avons fourni une visualisation d'un scénario temporel test (scénario relativement complexe) sans leur montrer la vue du source textuel. Nous leur avons alors demandé de nous décrire le scénario temporel correspondant et de nous expliquer son comportement. Les résultats ainsi obtenus ont permis de tirer plusieurs conclusions :
On peut dire que ces premiers résultats sont très encourageants mais restent à valider de manière plus rigoureuse.
Au cours de ce chapitre nous avons présenté les différents besoins liés à la visualisation graphique du scénario temporel en insistant sur les difficultés que soulèvent ces besoins (section 2). Nous proposons ensuite une solution qui, bien qu'elle ne réponde pas à tous les besoins évoqués, permet de poser un principe de base : visualiser à tout instant un placement temporel possible des objets et donner à l'auteur tous les moyens d'accéder simplement à tous les autres. Cette proposition a fait l'objet d'une mise en oeuvre en Tcl/Tk. Nous avons présenté (section 6) les algorithmes à la base de cette implémentation. Les résultats d'une première évaluation informelle de notre proposition terminent ce chapitre.
Les points importants qui se dégagent de cette solution sont :
Concernant la capacité de notre proposition à s'adapter à de gros volumes de données la solution que nous avons choisie pour intégrer la hiérarchie à la visualisation d'informations temporelles nous permet d'espérer des résultats satisfaisants. En effet l'auteur peut sans restriction fermer et ouvrir des niveaux de hiérarchie.