Chapitre 3

Contraintes

[Table des matières]

1 Introduction

La manipulation des contraintes n'est pas propre à la visualisation graphique du scénario temporel. Que ce soit pour la planification du scénario joué par l'interface de présentation de Madeus ou que ce soit pour le positionnement spatial des objets nous avons besoin de manipuler et de résoudre des systèmes de contraintes. Néanmoins notre problématique soulève des besoins particuliers notamment pour répondre au besoins mis en évidence dans le chapitre précédent.

Au cours de ce chapitre, après un bref rappel de la définition d'un système de contrainte (section 2), nous présenterons les besoins en terme de résolveurs de contraintes (section 3 ) définit à partir des besoins identifiés dans le chapitre II, avant de présenter les différentes approches pour résoudre de tels systèmes (section 4).

[Table des matières]

2 Résolution de contraintes

Définition d'un système de contraintes

Un problème de satisfaction de contraintes est la donnée d'un ensemble de variables dont les valeurs sont restreintes par des contraintes. Nous allons nous intéresser exclusivement aux CSPs binaires, c'est-à-dire ne manipulant que des contraintes entre deux variables, et au contexte classique dans lequel les contraintes sont discrètes. Le CSP à considérer est un triplé G={X,D,C}, où

- X ={x₁, ..., x_n} est un ensemble de variables,

- D = D₁ x ...x D_n représente les domaines de ces variables (ensembles de valeurs pouvant leur être affectées a priori),

- C = {c_ij / 1<= i,j <= n} est un ensemble de contraintes d'entrée.

Une contrainte c_ij exprimera la contrainte entre les variables x_i et x_j, restreignant du même coup les valeurs pouvant être prises simultanément par ces deux variables. Dans le cas fini, elle s'exprimera généralement sous la forme d'un ensemble de couples de valeurs permises.

c _ij = { (x_i1,x_j1), ..., (x_ip,x_jp) } subseteq D_i x D_j

Dans le cas des domaines infinis la contrainte est donnée en intention par un prédicat sur les variables de la contrainte.

On définit ensuite une solution d'un CSP comme étant une instanciation de toutes les variables satisfaisant l'ensemble des contraintes, c'est-à-dire:

Une solution est un ensemble delta = {x₁inD₁, ..., x_ninD_n / forallc_ijinC, (x_i,x_j)inc_ij}

Expression du scénario temporel sous forme de contraintes

Dans le cas d'un scénario temporel exprimé sous forme de contraintes, chaque objet est défini par deux variables (ses instants de début et de fin), le domaine de ses variables est [ 0, +infty ]. Chaque objet flexibles introduit une contrainte correspondant à son intervalle de durées possibles :

• BorneInf <= Fin - Début <= BorneSup

Et chaque relation du scénario est traduite en terme de contraintes qui sont toutes sous la forme d'une différence de la forme :

min <= X - X' <= max

min et max pouvant prendre leur valeurs dans l'intervalle [0.. infty [, et où X et X' sont des instants de début ou de fin.

Par exemple la relation During entre les objets 1 et 2 sera traduite par :

• 1 <= Fin2 -Fin1 <= + infty
• 1 <= Début1 - Début2 <= + infty

Satisfaction de contraintes ou maintien de solution

Etant donné un système de contraintes, on peut identifier deux problèmes différents :

• Satisfaction de contraintes

  On parle de satisfaction de contraintes lorsque l'on cherche à assurer la cohérence d'un système de contraintes et à trouver une ou toutes les combinaisons de valeurs des variables qui permettent de satisfaire l'ensemble des contraintes.

• Maintien de solution

  On parle de maintien de solution lorsqu'à partir d'une solution d'un système de contraintes et d'une perturbation de cette solution (soit par modification de la valuation d'une des variables, soit par ajout ou retrait d'une contrainte) on cherche à calculer une nouvelle solution. Dans ce cas, le système de contraintes est dit dynamique.

Notre problématique de visualisation du scénario temporel telle que nous l'avons présenté dans les deux premiers chapitres se situe clairement dans une problématique de maintien de solution d'un système de contraintes dynamiques. En effet à un instant donné on visualise une solution d'un ensemble de contraintes et on doit réagir à une perturbation qui dans le cas présent est la modification de la durée d'un objet. Les besoins utilisateur généralement mis en avant lors de l'étude de cette classe de problèmes est l'efficacité et la stabilité des solutions (ie, la nécessité de modifier le moins possible la solution courante). Nous allons voir dans la section suivante comment ils correspondent aussi à une réalité dans notre contexte mais aussi comment les besoins identifiés en appellent d'autres.

[Table des matières]

3 Les besoins

Nous allons voir dans cette partie comment les besoins identifiés dans le chapitre II se traduisent sur les algorithmes de maintien de solutions.

• Efficacité du calcul de la réponse

  Une qualité importante d'une interface est sa capacité à répondre rapidement aux actions de l'utilisateur. Une non-réponse du système dans un délai raisonnable peut amener l'utilisateur à se lasser et à ne plus utiliser le système ou il peut l'amener à répéter sa commande, ce qui peut avoir des effets indésirables. L'efficacité de la méthode de résolution est donc un facteur très important dans notre contexte. Cette efficacité se traduit généralement par l'utilisation de techniques incrémentales (ie, elles profitent de la solution courante pour calculer la nouvelle solution). Là où un résolveur non-incrémental reconsidérerait l'ensemble des contraintes, même en cas de moindre changement, un résolveur incrémental ne réévalue que les contraintes affectées par cette perturbation.

• Stabilité des solutions, minimisation du nombre d'objets modifiés

  Nous avons soulevé dans le chapitre II le problème de contrôle de la solution en cas de réponses multiples, ce besoins ce traduit par les deux points suivants :

  • Mesure de distance entre les variables

    Cela nécessite que le résolveur de contrainte permette l'utilisation d'une fonction de localité entre les variables. Par exemple on peut imaginer de définir une fonction mesurant la distance entre deux variables en tenant compte de l'existence d'une relation directe entre deux objets.

  • Priorité sur les variables à déformer

    Il est souhaitable que le système de contrainte puisse nous permettre de définir des priorités sur les variables à modifier, ou sur contraintes, ceci afin de pouvoir privilégier entre autre la déformation des délais par rapport aux autres objets.

• Connaissance de l'intervalle de validité d'une variable

  L'intervalle de validité d'une variable est l'ensemble des valeurs permises pour cette variable telles qu'il existe une valuation pour les autres variables qui rendent le scénario cohérent. Cette information nous permettrait d'anticiper la flexibilité des durées des objets.

[Table des matières]

4 Les solutions existantes

On peut diviser les méthodes de maintien de solution en deux catégories : les approches locales et les approches globales.

[Table des matières]

4.1 Les approches locales

Les résolveurs locaux utilisent un graphe de contraintes tel celui présenté dans la Fig 0 :

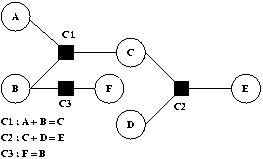
Fig 0. Graphe de contraintes

Le graphe de contrainte est construit de la manière suivante. Chaque variable du problème est représentée par un cercle, chaque contrainte est représentée par un carré, et chaque arc représente l'appartenance d'une variable a une contrainte. A chaque contrainte est associée un ensemble de méthodes qui explicite comment répercuter la modification d'une variable sur les autres variables présentes dans la contrainte. Par exemple, une méthode associée à la contrainte C1 peut être A <== C + B qui indique comment répercuter une modification de C et/ou B (ce sont les entrées de la méthode) sur A (c'est la sortie de la méthode).

C'est la technique de résolution la plus employée dans les applications graphiques. De nombreux travaux ont été fait sur le sujet et se poursuivent (ex : ThingLab et SketchPad ).

La fonction d'un résolveur local incrémental est de décider :

• les contraintes à réévaluer, seules celles qui risquent d'être violées par la perturbation et par ses conséquences sont reconsidérées, c'est en cela que ces techniques sont incrémentales.
• les méthodes à utiliser, pour chaque contraintes à réévaluer, il faut décider quelle est la méthode associée qui va permettre de la satisfaire à nouveau (en fonction des choix déjà effectués sur les autres contraintes).
• L'ordre dans lequel celles-ci doivent être appliquées afin de satisfaire à nouveau l'ensemble des contraintes.

La méthode la plus communément utilisée pour assurer ces trois fonctionalités est la méthode par propagation locale de valeurs . L'idée sous-jacente à cette technique est de dire que dès que la contrainte possède assez d'informations pour calculer des valeurs, elle les calcule. Elle se décompose en deux phases :

1. Une phase de planification au cours de laquelle le résolveur sélectionne une méthode pour chacune des contraintes à recalculer, et uniquement pour celles-ci. Cet ensemble de méthodes est calculé en partant de la variable perturbée et en identifiant toutes les contraintes potentiellement insatisfaite. Pour chacune de ces contraintes une méthode est choisie. Cette méthode doit prendre la variable perturbée en entrée et une variable ne doit pas être en sortie de deux méthodes. Ce choix construit un ensemble de variables modifiées par la perturbation initiale. Il faut donc calculer un nouvel ensemble de contraintes à réévaluer parmi les contraintes non encore examinées, et recommencer ainsi de suite jusqu'à ne plus avoir de contraintes à reconsidérer. L'ordre d'exécution correspond a un tri topologique de ce graphe en fonction de son orientation.

   Par exemple une orientation possible dans l'exemple de la Fig 0 est donnée dans la Fig 1 , cette orientation répercute une modification de A sur les variables C, D et F.

2. Une phase d'exécution pendant laquelle le plan constitué est exécuté en séquence . Dans cette phase, les valeurs connues sont propagées le long des arcs du graphe de contraintes.

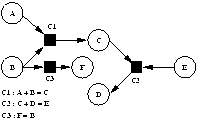
Fig 1. Orientation du graphe de contraintes

Les avantages de la propagation locale sont l'efficacité, la généricité et les facilité de compréhension du comportement des variables. Les désavantages bien connus de ces méthodes sont :

• L'incomplétude de la méthode lorsque par exemple le graphe de contrainte est cyclique. Par conséquent de tels systèmes rejettent les systèmes de contraintes qui introduisent des cycles. Dans notre contexte, les systèmes de contraintes que l'on manipule engendrent des graphes de contraintes fortement cycliques.

• La manipulation de contraintes uniquement fonctionnelles. Une contrainte à n variables est fonctionnelle, si lorsque l'on fixe n-1 variables, la dernière est déterminée de façon unique. Dans notre contexte, les contraintes qui limitent l'intervalle de validité d'une variable ne sont pas fonctionnelles.

Ces deux raisons sont suffisantes pour ne pas retenir ces méthodes dans notre contexte. Cependant les techniques employées, comme la définition de poids associés aux contraintes, pour contrôler la solution et orienter la recherche sont intéressantes et adaptable à notre problème. Pour ce qui est de notre besoin de connaître les domaines de validité des variables, nous n'avons à ce jour pas d'idée sur la façon d'obtenir ces informations en utilisant ces méthodes sauf par des essais successifs.

[Table des matières]

4.2 les approches globales

Nous venons de voir que les méthodes locales ne permettent pas de répondre complètement à nos besoins spécifiques. Nous étudions à présent l'autre type d'approche, les approches globales. On ne présentera qu'un seul algorithme de cette classe qui est représentatif de l'approche. Cet algorithme appelé Dynamic Backtrack est une adaptation de l'algorithme backtrack utilisé dans un problème de satisfaction statique de contraintes. Celui ci est présenté ci dessous.

L'algorithme de backtrack

Nous rappelons simplement les caractéristiques essentielles de cet algorithme. Dans l'état initial aucune variable n'est affectée. A une étape donnée l'ensemble des variables sera divisé en deux groupes, les variables affectées et les variables non affectées. La solution courante est cohérente avec l'ensemble de contraintes. L'étape va consister à affecter une nouvelle variable, le système choisi une variable et une valeur dans l'ensemble de celles possibles et vérifie la cohérence. Si le système est cohérent il passe à l'étape suivante, si le système est incohérent il essaie une autre valeur pour la variable considérée. Si toutes les valeurs ont été considérées il désaffecte une des variables affectées, et repart à l'étape n-1.

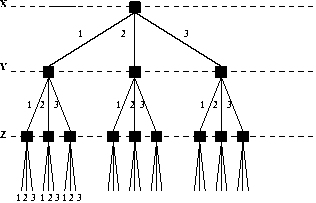
Fig 2. Arbre de recherche

Dans l'exemple de la Fig 2 on peut voir un arbre de recherche possible dans le cas où nous avons des contraintes qui portent sur trois variables X,Y et Z (chacune étant définie dans l'intervalle [1..3]).

C'est par exemple la méthode employée dans IlogSolver .

Retour arrière dynamique

Cet algorithme part d'une solution courante, son mécanisme est assez proche de la version de l'algorithme de backtrack présenter précédemment. Cet algorithme divise les variables en deux catégories: variables fixées et variables non fixées. Dans l'état initial aucune variable n'est fixée. A chaque étape toutes les variables sont valuées, et le système peut être ou non cohérent, mais la valuation des variables fixées est cohérente. A chaque étape le système cherchera à étendre l'ensemble des variables fixées. Des heuristiques sur le choix des variables à remettre en cause lors de retour arrière ou sur le choix des valeurs pour une variable sont réalisable, ce qui permet d'améliorer et de personnaliser cet algorithme de manière à orienter la recherche de solution. Par exemple on peut imaginer, dans notre cas, de désaffecter en priorité les variables représentant les instants de début et fin des délais.

L'avantage majeur de cette technique est sa complétude: on trouve toujours la solution si elle existe et la possibilité pour l'utilisateur de contrôler la recherche de solution en cas de réponse multiples.

Ses inconvénients sont :

• l'obligation de travailler sur des domaines finis, or nos systèmes de contraintes manipulent des domaines infinis.
• le coût généralement très grand de cette technique, qui procède par énumération, lorsque le domaine des variables est trop grand.

Cependant ces deux inconvénients peuvent être réduits par les deux remarques suivantes :

• Il est possible d'utiliser sur nos graphes temporels un algorithme de filtrage appelé PC2 qui va réduire les domaines de validité de toutes les variables aux valeurs qui apparaissent dans au moins une solution du système de contraintes, et donc de diminuer l'espace de recherche améliorant ainsi les coûts d'un algorithme de type backtrack dynamic. Un autre avantage de l'utilisation d'un algorithme de type PC2, et qu'il permet de connaître l'intervalle de validité des variables.
• Nous posons la conjecture suivante : toute modification élémentaire (+1 ou -1 unité) d'une variable se traduit par au plus une modification élémentaire sur les autres variables. Cette conjecture nous permet de limiter tous les domaines à des déformations élémentaires autour de la solution courante, éliminant ainsi le problème des domaines infinis. Cette conjecture bien entendu reste à démontrer.

[Table des matières]

5 Conclusion

Comme nous avons pu le voir au cours de ce chapitre aucune méthode de maintien de solution répond complètement à nos besoins :

• les méthodes locales du fait de leur incomplétude et par leur incapacité à manipuler des contraintes non fonctionnelles ;
• les méthodes globales du fait de leur manque d'efficacité.

Néanmoins dans le cas de approches globales nous avons quelques idées pour contourner ces difficultés, notamment avec l'application d'algorithmes de type PC2.

Un problème commun à toute ces approches (locale et globale) est quelles ne nous permettent pas d'anticiper l'intervalle de flexibilité. Il va dont être nécessaire de réaliser un algorithme qui nous permettra d'anticiper cette intervalle dans toutes les configurations possibles (déplacements locaux ou globaux) et de manière efficace.

Nous allons maintenant présenter une méthode ad'hoc qui nous permet de traiter de manière efficace une partie des besoins présentés ainsi que les choix de représentation graphique pour les concepts de flexibilité et d'interruption présentés dans le chapitre II.

Notes :