Comme nous l'avons dit dans le chapitre , nous avions besoin de maintenir localement la solution courante de notre ensemble de contraintes définissant le scénario temporel d'un document multimédia. De plus nous avons besoin de contrôler le système de résolution de manière à pouvoir définir des préférences sur les méthodes à utiliser ainsi que sur les objets à déformer. Dans l'attente de trouver un résolveur permettant de résoudre de façon plus générale (possibilité d'utiliser l'algorithme à la fois pour le placement spatial, placement temporel, et pour la résolution du système de contrainte), nous avons adapté et développé un algorithme réalisé dans le cadre du DEA et fondé sur l'utilisation du graphe temporel (qui peut être considéré comme le graphe de solution correspondant à l'ensemble des contraintes) plutôt que sur le graphe de contraintes de manière à utiliser pleinement la topologie du problème ainsi que de sa solution. Cet algorithme développé dans le cadre du DEA ne prenait en compte que les perturbations liées au déplacement d'un objet dans le représentation graphique du scénario temporel. Nous l'avons retravaillé afin de traiter le cas d'une perturbation par retaillage.
Dans un premier temps nous allons présenter le graphe temporel sur lequel repose nos algorithmes, dans un second temps nous présenterons nos algorithmes avant de présenter dans un troisième temps leur intégration et leur utilisation dans le système de visualisation graphique du scénario temporel.
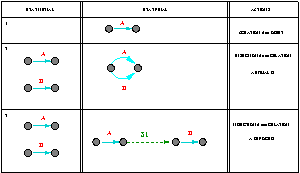
Le graphe temporel est un graphe acyclique orienté. Les noeuds sont les instants de début et de fin des intervalles. La présence d'un arc entre deux noeuds n1 et n2, traduit le fait que n2 se situe temporellement après n1. Les arcs sont étiquetés par 4 valeurs:
Pour expliquer la construction du graphe temporel (pour plus de détails voir ), nous allons donner l'idée de sa construction incrémentale.
Nous distinguons deux types d'actions :
L'objet est représenté pas un intervalle. Nous créerons donc un arc entre deux noeuds.
L'insertion d'une relation entre deux objets a pour effet de modifier le graphe temporel. Ces modifications peuvent être de deux types:

Fig 0. Construction du graphe temporel
Dans la Fig 1 nous présentons un exemple de graphe temporel.
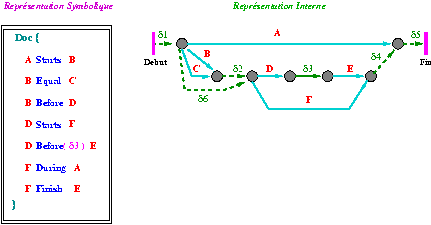
Fig 1. Le graphe temporel interne
L'objectif est de trouver à partir d'une solution donnée et d'une perturbation de l'auteur (retaillage ou déplacement) une nouvelle solution cohérente. De plus on veut pouvoir empêcher a priori toutes perturbations qui conduisent à un système incohérent.
Le premier algorithme que nous allons présenter est une optimisation de l'algorithme réalisé dans le cadre de mon DEA. Cet algorithme suppose l'existence d'une solution courante au système de contraintes, cette solution nous est donnée par exemple par l'utilisation d'un algorithme de type PathConsistency .
Que ce soit pour le déplacement ou le retaillage l'idée est la même : lorsque l'objet est sélectionné il faut calculer l'intervalle de déplacement ou de retaillage permis (c'est de cette manière que l'on sait a priori quelles sont les perturbations autorisées) ainsi que la liste des objets qui vont être modifiés (déplacement, retaillage) par la perturbation.
Il est important de noter que ces calculs ne se font qu'au moment de la sélection de l'objet, au cours du déplacement on ne fait que mettre à jour les informations graphiques pour l'affichage des objets. Ce principe nous permet d'obtenir de bonnes performances en temps.
L'idée générale de l'algorithme est de parcourir tous les chemins entrants ou sortants des deux noeuds de l'intervalle représentant l'objet sélectionné et de trouver, pour chacun de ces chemins, un objet amortissant les déplacement appliqués par l'auteur sur cet objet. Dans cette version, nous recherchons le premier délai flexible sur chaque chemin.
L'algorithme proposé se décompose en deux phases:
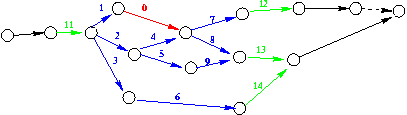
Fig 2. Parcours du graphe temporel
Par exemple, dans la Fig 2 nous représentons un exemple de parcours possible, l'objet sélectionné est en rouge, les objets qui vont se déplacer sont en bleu et les objets qui vont amortir le déplacement sont en vert. Dans ce cas les listes obtenues sont les suivantes:
Dans la seconde phase la deuxième liste sera divisée en deux :
L1 (respectivement L2) est la liste des objets qui vont s'allonger (respectivement se rétrécir) lors d'un déplacement à droite (respectivement à gauche) de l'objet sélectionné et se rétrécir (respectivement s'allonger) lors d'un déplacement à gauche (respectivement à droite).
Avant de présenter les algorithmes nous allons présenter rapidement certaines fonctions qui nous seront utilisées par la suite.
Variables Objet 1 (Noeud11,Noeud12) Objet 2 (Noeud21, Noeud22)
Renvoie vrai si L'objet 2 est à droite de l'objet 1. C'est a dire qu'il appartient soit a la liste des arcs entrant dans Noeud21 ou Noeud22.
Variable Objet1
Renvoie vrai si L'objet 1 est considéré comme un objet amortissant. Dans notre implémentation ce sont les objets de type délais flexibles, mais il est envisageable d'utiliser d'autres définitions pour généraliser l'algorithme.
Variable Objet1
Renvoie l'ensemble des objets qui sont en relation directe (il existe une contrainte directe) avec l'objet 1 (ie : il existe une contrainte qui lie les instants de début et/ou de fin des deux objets)
Variable Objet1
Renvoie l'ensemble des objets qui sont en relation directe (il existe une contrainte directe) avec la fin de l'objet 1 (ie : il existe une contrainte qui lie les instants de fin des deux objets)
Nous allons maintenant présenter l'algorithme qui identifie les objets affectés par le déplacement de l'objet sélectionné:
Fonction : IdentificationDesObjetsAffectés
Variables
Entrées :
ObjetSel
LObjetsAmortis
LObjetsDeplacés
Locales :
Objet
Sorties :
LObjetsAmortis
LObjetsDeplacés
Début
PourChaque Objet enRelationAvec ObjetSel
Si neg EstMarqué(Objet) alors
Marquer(Objet)
Si Type(Objet) in TypeAmorti alors
Objet ==> LObjetsAmortis
Sinon
IdentificationDesObjetAffectés
(Objet,LObjetsAmortis,LObjetsDéplacés)
Objet ==> LObjetDeplace
Fin Si
Fin Si
Fin Pourchaque
Fin
Nous allons maintenant présenter la fonction qui permet de classer les objets affectés :
Fonction : Classification :
Variables
Entrées :
ObjetS
LObjetsAmortis
LObjetsDeplacés
Locales :
Objet
Sorties :
LAmortiD
LAmortiG
Début
PourChaque Objet de LObjetsAmortis
Si exists O telque
(O in LObjetsDeplacés et
Adroite(O, Objet)) alors
Objet ==> LAmortisD
Sinon
Objet ==> LAmortisG
Fin Si
Fin Pourchaque
Fin
L'algorithme pour le redimensionement des objets est fortement inspiré de cet algorithme, seul la première passe est différente. Lors du calcul des objets affectés il faut gérer une détection des cycles dans le graphe temporel. De plus le premier appel est différent des autres, en effet on ne lance la récursivité que sur un des deux noeud de l'objet sélectionné en fonction de la manipulation effectuée.
Nous allons maintenant présenté le premier appel pour la recherche des objets affectés par la manipulation, la récursivité se fera sur une fonction très similaire à la première étape présentée précédemment avec en plus le test pour la détection des cycles.
Variable Objet
Renvoie vrai si on est sur un cycle et tous les autres objets appartenant a ce cycle sont marqué.
Fonction : Premiere_Etape_Retaillage
Variables
Entrées :
ObjetS
LObjetsAmortis
LObjetsDeplacés
Locales :
Objet
Sorties :
LObjetsAmortis
LObjetsDeplacés
Début
Si RetaillageBordDroit alors
L <== EnRelationAvecLaFinDe ObjetS
sinon
L <== EnRelationAvecLeDebutDe ObjetS
FinSi
PourChaque Objet de L
Si negEstMarqué(Objet) alors
Marquer(Objet)
Si (Type(Objet) in TypeAmorti
ou DetectionCycle) alors
Objet ==> LObjetsAmortis
Sinon
IdentificationDesObjetsAffectés (Objet, LObjetAmortis,
LObjetsDéplacés)
Objet ==> LObjetDeplacés
Fin Si
Fin Si
Fin Pourchaque
Fin
Dans les deux cas le coût de l'algorithme est de l'ordre de O(n) avec n le nombre d'objets (objets + délais) du graphe au niveau de hiérarchie courant, ce qui est très satisfaisant.
Cette solution répond à trois des critères que nous avons identifiés :
Néanmoins cet algorithme suppose que les déformations se limitent au niveau de hiérarchie courant. Ce choix a été fait dans le souci de limiter les perturbations visuelles en permettant ainsi à l'auteur de prévoir et de comprendre toutes les modifications effectuées.
Cette solution ne permet pas de :
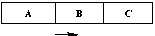
Fig 3. Impossibilité de répercuter simultanément les déformations sur 2 objets
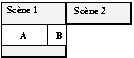
Fig 4. Impossibilité de répercuter simultanément les déformations sur 2 niveaux de hiérarchie différents
Dans les deux cas, pour résoudre ces problèmes, on peut imaginer un mécanisme qui permettrait d'appeler plusieurs fois de suite l'algorithme actuel, et qui puisse connaître les objets indéformables pour une manipulation donnée. Cependant connaître cette information a priori n'est pas triviale et risquerait d'entraîner une importante dégradation des performances.
Nous venons de voir que nous avons maintenant à notre disposition un algorithme qui nous permet de manipuler la flexibilité des objets. Nous allons donc nous intéresser maintenant à l'intégration de cette flexibilité dans le système de visualisation.
Dans le souci de ne pas surcharger la représentation graphique, et de respecter l'honnêteté temporelle nous avons choisi d'utiliser deux métaphores graphiques pour représenter cette flexibilité.
La première qui consiste à représenter explicitement les bords retaillables des objets, cette représentation est toujours présente à l'écran. La seconde consiste à changer le curseur de la souris pour montrer à l'auteur qu'il peut retailler l'objet. Cette métaphore, contrairement à la première n'est donc présente que lorsque le curseur souris est sur un des bords retaillable de l'objet.
Dans l'exemple de la Fig 5 nous pouvons voir l'affichage avant et après manipulation de la flexibilité de l'objet Texte 3. L'auteur a agrandi de 1 cet objet par la droite. Le scénario s'est adapté à cette modification de façon continue, et nous pouvons voir que tous les objets flexibles sont facilement identifiables.

Fig 5. Manipulation de la flexibilité des objets
L'algorithme décrit dans la section précédente a identifie l'objet à déformer et a répercuter les déformations nécessaires pour compenser l'agrandissement de l'objet Texte3.
Comme pour la visualisation des relations d'Allen (section 0.0) nous avons choisi de représenter explicitement les opérateurs d'interruption (comme nous l'avions suggéré dans le chapitre II).
Nous représentons aussi explicitement les objets coupés (par une représentation en grisé) de manière à ce que l'auteur puisse se rendre compte que des objets n'ont potentiellement pas totalement délivrés leur contenu sémantique.
Sur l'exemple de la Fig 8 nous pouvons voir la représentation de l'opérateur Parmin pour les objets définis dans la Fig 6 et les relations définies dans la Fig 7 . Nous pouvons aussi voir explicitement la partie des objets interrompue.
|
Objets Objet 1 Objet 2 Objet 3 Objet 8 Objet 10 Délai Before |
Durées
|
Fig 6. Relations entre les objets et durées des objets
Relations
Objet 1 Start Objet 8
Objet 1 Parmin Objet 2
Objet 1 Start Objet 10
Objet 1 Before Objet 3
Objet 2 Equal Objet 10
Fig 7. Scénario
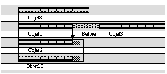
Fig 8. Visualisation des opérateurs d'interruption
La représentation graphique de la flexibilité permet à l'auteur de savoir quels sont les objets déformables, mais aussi quelles sont les manipulations qu'il peut effectuer sur le scénario courant.
La représentation des opérateurs d'interuption permet elle d'anticiper le comportement du scénario et de comprendre la solution courante, tout en ayant la connaissance des effets de l'interruption, notamment sur les objets interrompus.
La solution algorithmique proposée pour la déformation de solution a permis de tester les idées graphiques, mais il faut chercher une solution plus générale, notamment pour permettre des déformations globales et intégrer des déformations sur plusieurs niveaux de hiérarchies.