
Chapitre V : Les contraintes au coeur
de l application
1.Introduction
Au cours du chapitre III, nous avons choisi de fournir un formalisme
d'édition à l'auteur qui était une combinaison d'un formalisme relationnel
prédictif et du formalisme du langage multimédia utilisé pour stocker le
document. Nous avons vu, dans le chapitre IV, que les structures de données de
Kaomi ont été réalisées de manière à stocker les informations liées à ces deux
types de formalismes.
Dans ce chapitre, nous allons nous intéresser à l'implémentation des
services d'aide, et plus particulièrement aux services de cohérence et de
formatage pour le formalisme relationnel offert dans Kaomi. Nous verrons dans
le chapitre VI, quelles extensions ou améliorations seront nécessaires pour
étendre les mécanismes proposés dans ce chapitre de manière à réaliser le
formatage et la vérification de cohérence pour un formalisme non relationnel
et/ou imprédictif.
Au cours de cette thèse nous avons fait le choix d'étudier des solutions
qui s'appuient sur des techniques de résolution de contraintes pour mettre en
oeuvre les services de cohérence et de formatage plutôt que de chercher des
solutions ad hoc, nous détaillerons cette justification ci-après. L'objectif
de ce chapitre est double : trouver un ou plusieurs résolveurs de contraintes
adaptés à nos besoins et les intégrer dans la boîte à outils Kaomi.
L'organisation de ce chapitre est la suivante :
Dans une première étape, nous allons justifier notre intérêt pour les
résolveurs de contraintes dans Kaomi (section 2) et présenter les différentes
manières d'intégrer un résolveur de contraintes à une application (section
3).
Dans une deuxième étape, nous présenterons le mécanisme général de
fonctionnement d'un résolveur de contraintes (section 4) pour nous intéresser
plus particulièrement au processus de traduction de nos données vers les
points d'entrée de ces résolveurs (section 5).
Dans une troisième étape, nous chercherons le résolveur idéal pour notre
contexte. Pour cela, nous présenterons les différents types de résolveurs
existants en les classant par rapport à leurs mécanismes de résolution
(section 6). Nous chercherons ensuite à évaluer ces différents résolveurs tant
d'un point de vue qualitatif que quantitatif dans un contexte d'édition. Pour
cela, nous présenterons, dans un premier temps, comment s'effectue
l'intégration d'un résolveur de contraintes dans Kaomi (section 7) et dans un
deuxième temps les résultats tant qualitatifs que quantitatifs de l'évaluation
des différents résolveurs (section 8).
Enfin, pour conclure ce chapitre nous ferons un bilan sur l'apport des
contraintes dans la réalisation et l'utilisation d'un environnement auteur de
documents multimédias.
2. Utilisation des contraintes
Dans toutes tâches de conception où l'on peut séparer la phase de
spécification et la phase de réalisation, il peut être intéressant d'utiliser
des mécanismes à base de contraintes pour chacune de ces phases. En effet,
l'utilisation des techniques à base de contraintes permet :
- Au niveau de la spécification,de simplifier le travail de
l'utilisateur (auteur) en lui fournissant un modèle de spécification
simple (déclaratif) et paramétrable. Cela permet de dégager
l'utilisateur de la résolution de sa spécification.
- Au niveau de la réalisation,de simplifier le travail du
développeur d'une application en lui fournissant des mécanismes
automatiques de résolution de la spécification de l'auteur (qu'elle soit
spécifiée en terme de contraintes ou pas).
Dans ces deux catégories d'utilisation des travaux probants ont permis de
valider l'utilisation de ces techniques dans un contexte applicatif.
La première catégorie d'utilisation concerne la spécification par l'auteur
d'une entité (document, interface) à l'aide de contraintes :
- Spécification du scénario temporel: l'auteur spécifie un
ensemble de relations entre les objets. C'est le cas de la spécification
du scénario temporel dans Nsync [Bailey98]. La résolution des
contraintes, réalisée par un module externe (Berkeley Continuous Media
Toolkit) se fait au début de présentation, et permet calculer le
placement temporel de tous les objets.
- Spécification de pièces de musique: dans le logiciel de
composition musicale appelé Boxes [Beurivé00], l'utilisateur place des
sons les uns par rapport aux autres dans le temps. Il peut les organiser
hiérarchiquement (pour obtenir des mélodies ou des pièces de musique),
mais il peut aussi déclarer des relations temporelles entre ces
éléments. Le résolveur Cassowary [Badros98] est utilisé pour résoudre la
spécification de l'auteur.
- Spécification de documents. Parmi les utilisations des
contraintes pour la spécification de documents multimédias on peut citer
Anecdote [Harada96], ISIS [Kim95], Madeus [Layaïda97], et les travaux de
Saade [Saade97] qui proposent une édition de documents avec des
contraintes spatiales et temporelles.
- Spécification d'interfaces graphiques : de nombreux outils
permettent de spécifier des interfaces via des mécanismes proches des
contraintes. Par exemple, le langage Java permet de définir des
composants graphiques avec des politiques de placement pour les objets à
l'intérieur du composant. C'est le système qui, au moment de
l'affichage, s'occupera de calculer les positions absolues des
différents objets en résolvant les contraintes spécifiées par l'auteur.
De la même façon, le système Scwm [Badros00] permet à l'auteur de
spécifier un ensemble de relations entre les différents objets composant
l'interface.
- Le dessin d'objets géométriques : dans le cas de Cabri II
[Laborde95], les contraintes sont utilisées à la fois pour spécifier les
relations spatiales entre les objets mais aussi pour maintenir des
propriétés géométriques sur les objets et entre les objets, notamment
lors des manipulations de l'utilisateur. Charman [Charman94] utilise lui
les contraintes pour l'aide à l'aménagement spatial d'objets (définition
de plan par exemple).
La deuxième catégorie d'utilisation des technologies à base de contraintes
concerne la résolution d'une spécification (qui n'est pas forcement exprimée
sous forme de contraintes). Ces techniques permettent au programmeur de
l'environnement de se dégager de la résolution, et du maintien des relations
en utilisant des résolveurs externes. Parmi les principales utilisations, on
peut citer :
- L'affichage de champs d'étoiles: dans l'outil StarGen
[Hudson95], l'auteur spécifie un ensemble de valeurs à afficher dans des
structures de données abstraites. Le système StarGen traduit cet
ensemble de valeurs en un ensemble de contraintes qui seront résolues
par un résolveur de contraintes externe, pour être finalement affichées
à l'écran.
- Pour la spécification d'animation: on peut citer les travaux de
TRIP [Takahashi95] où l'auteur peut spécifier des représentations
graphiques de données arborescentes mais aussi des animations graphiques
en 2D et 3D au moyen de langages abstraits qui sont ensuite convertis en
un ensemble de contraintes spatiales permettant de définir l'affichage
des objets à l'écran. Cet ensemble de contraintes est ensuite résolu par
le résolveur Detail [Hosobe98].
Dans le cadre de l'édition de documents multimédias nous avons vu qu'il était
intéressant de séparer la spécification du comportement temporel et spatial du
document de la phase de calcul du placement absolu des objets. Des expériences
positives ont eu lieu au sein du projet Opéra ([Carcone97] et [Carcone97b])
pour calculer le placement spatial d'objet. Au cours de cette thèse nous avons
eu la volonté d'apporter une réponse globale au problème de formatage et de
vérification de cohérence dans le contexte de l'édition de documents
multimédias.
Dans Kaomi, les résolveurs sont utilisés pour réaliser les fonctions
suivantes :
- Vérification de l'existence de solution, et calcul de l'espace de
solutions.
- Propagation des modifications de l'auteur lors de l'édition.
- Maintien des relations et de la cohérence de l'affichage lors des
manipulations de l'auteur (formatage lors des déplacements d'objets dans
la vue temporelle ou de présentation).
Ces différentes fonctions interviennent principalement dans trois modules
suivants de Kaomi ( Figure V-1) :
- Le module de visualisation, qui permet par exemple de visualiser
l'espace de solutions.
- Le module d'édition, qui après chaque opération d'édition de l'auteur
doit assurer la cohérence et le formatage du document.
- Le module d'aide qui au cours des manipulations de l'auteur dans les
vues temporelle ou de présentation doit calculer un nouveau placement
pour les objets.
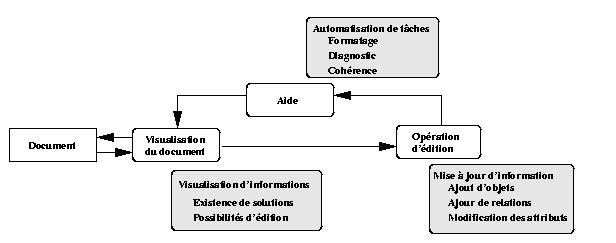
Figure V-1 : Les contraintes dans l'édition
3. Les différentes approches pour choisir ou créer
un résolveur
Il existe de nombreuses manières d'aborder la résolution de contraintes :
- Les langages de construction de résolveurs : dans ces approches
l'utilisateur décrit (programme) dans un langage spécialisé le résolveur
de contraintes qu'il désire obtenir. Cette approche est illustrée par
Laure [Caseau94] et Claire [Caseau96]. L'utilisateur doit intégrer des
mécanismes de bas niveau pour créer un résolveur, le langage lui
fournissant par exemple le moyen de stocker l'état courant des
variables. Il peut, par exemple, définir ainsi une contrainte qui
vérifie que pour chaque élément x, la date minimale de début de
x et inférieure à la date maximale de début de x.
[define checkconstraint
constraint
for_all x:integer,
y:integer,
if [exist z, atleast(z) =x ,
atmost(z) = y]
check x <= y
]
Cette approche nécessite une bonne connaissance des mécanismes de
résolutions de contraintes pour réaliser un bon résolveur. Cependant les
résolveurs produits sont spécifiques pour un problème particulier et
efficaces.
- Les librairies: ces librairies fournissent un ensemble de
contraintes génériques ainsi que le mécanisme de résolution adapté qui
peuvent être utilisés dans un large éventail de situations.
L'utilisateur de telles librairies doit traduire son problème dans le
formalisme de contraintes offert par la librairie. Cette traduction,
selon le problème et la librairie peut être une tâche difficile. Les
contraintes globales de CHIP [Beldiceanu94, Aggoun93] sont une
illustration de telles librairies. Les résolveurs sont génériques et en
général simples d'utilisation, cependant leur efficacité fluctue en
fonction du domaine d'application.
- Les librairies extensibles: ces librairies fournissent les
services d'une librairie de contraintes, mais permettent aussi à
l'utilisateur de les spécialiser pour un domaine particulier. L'intérêt
de telles approches est qu'elles permettent immédiatement au programmeur
d'utiliser le résolveur, tout en lui permettant de l'étendre ou de le
spécialiser pour son utilisation si le besoin s'en fait sentir
[Badros98].
Dans un contexte d'édition de documents multimédias, nous n'avons pas une
spécification du problème unique que nous résolvons en changeant seulement les
valeurs possibles des variables. Nous avons une spécification du problème
différente à chaque étape du processus d'édition (chacune des spécifications
étant proche de la précédente). De ce fait nous avons choisi d'étudier plus
précisément les deux dernières approches qui semblent plus flexibles en
permettant plus facilement le changement incrémental de la spécification du
problème.
4. Mécanisme général de résolution de
contraintes
Un résolveur de contraintes est un programme qui à partir d'un ensemble de
contraintes calcule une solution (si elle existe) satisfaisant toutes les
contraintes.
Nous allons donc dans un premier temps présenter les CSP (Constraints
Satisfaction Problem) qui permettent de représenter l'ensemble de contraintes
manipulé par les résolveurs de contraintes, et dans un deuxième temps nous
définirons la notion de solution d'un CSP.
Un problème de satisfaction de contraintes est la donnée d'un
ensemble de variables dont les valeurs sont restreintes par des contraintes.
Nous allons nous intéresser exclusivement aux CSP binaires, c'est-à-dire aux
CSP ne manipulant que des contraintes entre deux variables.
Le CSP à considérer est un triplé G={X, D, C}, où :
- X ={X1, , Xn} est un ensemble de variables,
- D = D1 ´ ´ Dn représente les domaines de ces variables
(ensembles de valeurs pouvant leur être affectées a priori),
- C = {Cij / 1<= i,j <= n} est un ensemble de contraintes
d'entrées.
Une contrainte Cij exprimera la contrainte entre les variables
Xi et Xj, restreignant du même coup les valeurs pouvant
être prises simultanément par ces deux variables. Dans le cas fini, elle
s'exprimera généralement sous la forme d'un ensemble de couples de valeurs
permises.
C ij = { (Xi1, Xj1), , (Xip,
Xjp) } sur l'espace Di ´
Dj.
Dans le cas des domaines infinis, la contrainte est donnée en intention par
un prédicat sur les variables de la contrainte.
On définit ensuite une solution d'un CSP comme étant une
instanciation de toutes les variables satisfaisant l'ensemble des contraintes,
c'est-à-dire :
une solution est un ensemble D = {X1
dans D1, , Xn dans Dn / pour tout
Cij dans C on a (Xi, Xj) dans
Cij}.
On dit qu'un système est sous contraint lorsque l'ensemble des contraintes
n'est pas suffisant pour définir une solution unique au CSP.
L'expérience nous montrera plus tard que dans un système auteur nous avons
de tels systèmes du fait qu'un auteur ne spécifie pas un ensemble de
contraintes suffisant pour cela. Notons que c'est ce qui fait la force d'un
environnement auteur à base de contraintes, l'auteur ne spécifie que
partiellement son document laissant la tâche de calculer le placement spatial
et temporel des objets à l'environnement auteur.
Le système de résolution a donc le choix parmi un ensemble de solutions. Se
pose alors le problème de la pertinence de la solution choisie par rapport à
la spécification de l'auteur. De ce fait, il est nécessaire de donner des
informations supplémentaires au résolveur pour orienter le calcul d'une
solution. Ces informations peuvent être assimilées à des préférences de
l'auteur ou du système auteur vis-à-vis du résolveur pour l'aider dans son
choix de la solution.
Ces préférences peuvent être données sous trois formes (voir Figure
V-2):
- Complément d'information sur les données d'entrée, avec par exemple,
l'ajout de contraintes ou de priorités sur les contraintes pour orienter
la recherche de solutions.
- Contrôle sur le mécanisme de résolution, avec par exemple la
définition d'heuristiques sur la méthode de résolution.
- Contrôle sur les solutions produites, avec par exemple, un choix d'une
solution parmi un ensemble de solutions trouvées.
Nous verrons plus précisément ces techniques dans la section 5.3.
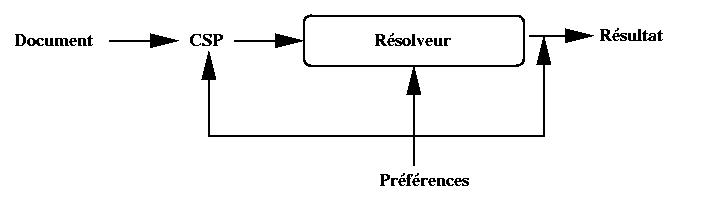
Figure V-2 : Orientation du processus de résolution
5. Traduction de notre problème vers un
CSP
L'objectif de cette section est de savoir quelles sont les contraintes qui
doivent être données en entrée du résolveur. Pour cela, nous avons besoin
d'une part de voir quelles informations du document doivent se traduire en
contraintes (section 5.1), et d'autre part analyser l'influence du cycle
d'édition sur le mécanisme de résolution (section 5.2). Nous verrons comment
cette influence se traduira vis-à-vis du résolveur (section 5.3).
5.1 Traduction des informations contenues dans le
document vers un CSP
Dans le cadre de l'édition de documents multimédias nous avons deux éléments à
modéliser :
- Définition des attributs des médias (X, Y, Début, Fin, ..) en
variables ;
- Traduction des relations et des événements en contraintes.
Au cours de cette section, les propositions que nous allons faire s'appliquent
aux dimensions temporelle et spatiale. Nous illustrerons indifféremment chacun
des aspects soit à l'aide d'un exemple temporel, soit d'un exemple spatial.
5.1.1 Expression des attributs temporels et spatiaux
dans un CSP
Dans le cas d'un scénario temporel exprimé sous forme de contraintes, chaque
objet (ou élémentTemporel) est défini par trois variables (Début, Fin et
Durée). Le domaine de ces variables est [0, +¥ [
È [?]. La valeur [?] indique que la variable n'est
pas affectée. Chaque variable flexible introduit une contrainte correspondante
à son intervalle de durées possibles (BorneInf £
Variable £ BorneSup). Une contrainte supplémentaire
permet de conserver la sémantique des variables (début + durée = fin).
Dans le cadre du scénario spatial, chaque objet est défini par six
variables : Haut, Bas, Gauche, Droite, Largeur, Hauteur, chacune étant définie
dans un intervalle de valeur ([0, +¥ [ È [?]). Ainsi, chaque variable flexible introduit une
contrainte correspondante à son intervalle de valeurs possibles (BorneInf
£ Variable £ BorneSup).
De plus, deux contraintes entre les variables (Gauche + Largeur = Droite et
Bas + Hauteur = Haut) expriment leur sémantique.
5.1.2 Traduction des relations en terme de
contraintes
Comme nous l'avons montré dans le chapitre IV (section 4.4.3), les relations
temporelles et spatiales sont converties en rélems. La conversion de relations
en rélems se fait à chaque ajout ou retrait de relations. Nous allons donc
nous intéresser maintenant au processus de conversion de ces rélems en terme
de contraintes.
Les rélems sont directement exploitables par les résolveurs de contraintes.
En effet, chacun des rélems (<, =, D ) se
traduit directement en termes de contraintes.
Dans l'exemple de la Figure V-3, on peut voir des exemples de telles
conversions. La principale difficulté vient des relations "Þ " et "Ü " qui ont un
comportement assimilable à un comportement d'interruption. Nous rappelons que
Début A Þ Début B signifie : si A est joué, alors
le début de A déclenchera le début de B. Comme nous sommes dans un contexte
déterministe, nous pouvons savoir statiquement si l'objet A est joué ou non.
Pour cela il suffit de résoudre le système, si A est joué on rajoute la
contrainte A.Début = B.Début.
Nous avons choisi d'insérer une nouvelle variable FinEffective, en plus des
trois variables temporelles précédentes, pour représenter les valeurs prises
lors de l'exécution, valeurs qui sont potentiellement différentes des valeurs
choisies statiquement par le formateur à cause des relations
d'interruption.
Ce choix, permettra par exemple dans la vue temporelle de représenter
explicitement la valeur prévue statiquement par le résolveur, et de visualiser
en même temps la valeur réelle prise par le média du fait de l'interruption
(rapport d'exécution).
|
Rélem
|
Contraintes
|
| Fin A ³
Début B |
C1:= A.Fin ³ B.Début |
| Début A £ Début B |
C2:= A.Début £ B.Début |
| Début A = Début B |
C3:= A.Début =
B.Début |
| Début A = Début B + t |
C3:= A.Début = B.Début +
t |
| Début A Þ Début B |
Si A est joué :
C5:= A.Début = B.Début
|
| Début A Ü Fin B |
Si B est joué :
C6:= B.FinEffective = A.Début
B.Fin > B.FinEffective
|
| Fin A Ü
Fin B |
Si B est joué :
A.FinEffective = B.FinEffective
et A.FinEffective < A.Fin
|
Figure V-3 : Conversion rélem-contraintes
L'ensemble des variables définies dans le document est introduit dans le
résolveur, ainsi que les contraintes déduites des rélems.
Comme pour les relations et les rélems, nous stockons les contraintes dans
le système et, plus particulièrement, dans le résolveur. Nous gardons un lien
pour chaque relation vers les rélems qu'elle a engendrés. Nous gardons aussi
pour chaque rélem la liste des contraintes qu'il a créés. De cette manière, à
chaque retrait de relation nous connaissons les rélems et les contraintes à
supprimer. Il est également très facile dans le cas d'une contrainte
insatisfaite de retrouver la relation qui l'a induite.
5.1.3 Traduction des événements en
contraintes
Dans le chapitre IV (section 4.4.6), nous avons vu comment traduire les
différents types d'événement dans notre formalisme d'édition. On peut noter
que dans le cas où les objets sont prédictifs et tous les événements
prédictifs alors ils sont traduisibles en termes de rélem. Or nous sommes dans
le formalisme relationnel prédictif offert par Kaomi. Les événements sont donc
traduits sous la forme des rélems "Þ " et "Ü ", et introduits dans le résolveur de contraintes.
Dans le cas où nous pouvons évaluer statiquement la valeur des variables
correspondante à la liste des dates d'occurrences d'un événement,
l'intégration des événements dans le résolveur se fait facilement. Il suffit
en effet de transformer chacune des instances d'occurrence de l'événement en
une nouvelle variable du résolveur.
Par exemple, l'événement :
Source = B
Destination = A
NbOccurence = 1
Date d'occurrence= {t tel que B se
termine}
Conditions = { }
Actions = {A.jouer
}
sera traduit par le rélem : B.Fin Þ A.Fin
et donc par les contraintes :
A.FinEffective = B.FinEffective et A.FinEffective < A.Fin
5.2 Influence du cycle d'édition sur le mécanisme de
résolution
Nous avons soulevé dans les chapitres II (section 2.2) et V (section 4) la
nécessité de contrôler le choix de la solution en cas de problèmes sous
contraints. Dans notre contexte d'édition, celle-ci engendre des besoins
précis que doivent satisfaire les résolveurs de contraintes :
- Prise en compte de préférences de l'auteur : l'auteur d'un
document multimédia intervient de manière directe dans le formatage de
son document. Par exemple, il peut vouloir spécifier une valeur préférée
sur ses médias. Le système de contraintes devra permettre de prendre en
compte de telles préférences qui sont explicitement demandées par
l'auteur.
Par exemple, les trois politiques de formatages suivantes peuvent être
pertinente dans un contexte d'édition de documents multimédias :
- Privilégier la déformation des délais par rapport aux autres
objets.
- Tenir compte du scénario temporel, par exemple, si l'auteur définit
une séquence de deux objets qui dure 10 secondes, et que chacun des
objets a un intervalle de durées possibles de [1,10], il est intéressant
pour l'auteur que le système de contraintes évalue la durée de ces deux
objets à 5 secondes.
- Tenir compte des valeurs intrinsèques des objets. Par exemple si le
premier objet est une vidéo avec une durée intrinsèque de 6 secondes et
le deuxième une image, alors le résolveur de contraintes évalue le
premier objet à 6 secondes et le second à 4 secondes.
On peut voir au travers de ces exemples, que pour un même problème il
existe plusieurs solutions de formatage qui peuvent être pertinentes
suivant le contexte. L'auteur doit donc aider le système vis-à-vis de ces
préférences.
- Maintien de proximité vis-à-vis de la solution courante. De par
les opérations d'édition de l'auteur, le document est en constante
évolution. Cependant, il est important que le système auteur ne change
pas complètement à chaque opération d'édition le document (les solutions
temporelle et spatiale associées au document). C'est pour cela que le
résolveur de contraintes doit être capable de prendre en compte cette
caractéristique, et permettre une certaine localité dans le calcul des solutions.
- Connaissance dela flexibilité dans le document (ou dans le
système de contraintes) : comme nous avons pu le voir dans le
chapitre III (section 3.3.2), il est important pour l'auteur de
connaître la flexibilité du document. L'intervalle de validité d'une
variable est l'ensemble des valeurs permises pour cette variable tel
qu'il existe une valuation pour les autres variables qui rende le
scénario cohérent.
De manière indépendante aux besoins qui viennent d'être cités, notons que dans
un contexte d'environnement interactif l'efficacité de la méthode de
résolution est un facteur très important. Cette efficacité se traduit
généralement par l'utilisation de techniques incrémentales (elles profitent de
la solution courante pour calculer la nouvelle solution). Là où un résolveur
non-incrémental reconsidérerait l'ensemble des contraintes, même en cas de
moindre changement, un résolveur incrémental ne réévalue que les contraintes
affectées par la dernière perturbation.
5.3 Recherche de la meilleure
solution
Les deux premiers points évoqués ci-dessus montrent bien qu'un besoin
essentiel pour un environnement auteur est d'obtenir une solution pertinente
(quand elle existe) pour l'ensemble des relations définies par l'auteur. Cette
solution est utilisée pour afficher le document dans la vue de présentation et
pour la jouer dans le temps. Le document défini par l'auteur peut produire un
large ensemble de solutions et le système de contraintes doit en choisir une
dans cet ensemble selon le critère de pertinence.
Cela pose dans un premier temps le problème de la définition de ce critère,
en effet celui ci dépend du contexte d'édition et dans un deuxième temps cela
nécessite l'utilisation d'un résolveur pouvant prendre en compte ce critère
dans sa recherche de solution.
Nous avons vu dans la section 5.2 que l'auteur pouvait en fonction du
contexte, vouloir exprimer différentes préférences. On voit, au travers de ces
exemples, que la notion de bonne solution n'est pas évidente, et qu'elle
dépend énormément du contexte et du souhait de l'auteur.
Le système auteur (aidé par l'auteur) doit donc guider le résolveur de
contraintes vers une bonne solution.
Il existe deux manières de guider les résolveurs de contraintes. La
première consiste en l'utilisation de contraintes hiérarchiques [Borning87],
la seconde utilise une heuristique. Le choix entre les deux méthodes dépend du
résolveur, dans la section 6, nous préciserons pour chaque résolveur la
méthode d'orientation qu'il offre.
Nous venons de voir qu'il était important d'obtenir la meilleure solution.
Encore faut-il être capable d'évaluer la qualité d'une solution. Dans ce but,
nous allons maintenant définir une fonction d'évaluation, qui va nous
permettre de mesurer un critère de qualité d'une solution (section 5.3.1).
Nous présenterons ensuite les deux manières d'orienter les résolveurs de
contraintes de façon à maximiser ce critère (section 5.3.2 et section
5.3.3).
5.3.1 Définition d'une fonction de
distance
Cette fonction de distance servira d'une part à orienter les résolveurs de
contraintes et d'autre part lors de l'étude des différents résolveurs de
contraintes pour évaluer la qualité des solutions proposées.
Pour répondre au besoin de proximité entre solutions successives on définit
la qualité d'une solution S2, obtenue après une action
d'édition de l'auteur appliquée sur une variable V, par sa distance par
rapport à la solution précédente (appelée S1).
Le premier paramètre (appelé P1) qui peut être pris en compte
pour la définition de cette fonction est celui de la distance entre la
variable V modifiée par l'auteur et les variables modifiées par le système
dans S2 pour mettre le système dans un état cohérent. On peut donc
définir la distance entre deux variables comme le nombre de contraintes entre
ces variables dans le graphe de dépendances (Figure V-4). Le graphe de
dépendance est construit de la manière suivante :
- Les variables du jeu de contraintes représentent les noeuds.
- Pour toutes les contraintes qui impliquent au moins deux variables, on
ajoute un arc entre chaque couple de noeuds représentant les variables de
la contrainte.
Par exemple, si nous avons les cinq contraintes ci-dessous représentées par le
graphe de dépendance de la Figure V-4 :
(A > B + C), (C > D), (B = E + F), (E = G), (G = D)
La distance entre les variables A et D est : distance(A, D) = 2.
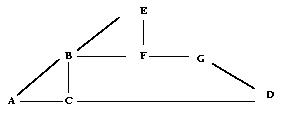
Figure V-4 : Mesure de la distance entre deux variables
Une telle notion de distance dépend évidemment du jeu de relations définies
entre les objets. Intuitivement on peut voir que l'objectif de minimiser ce
paramètre est de favoriser en priorité des modifications.
D'autres paramètres peuvent être utilisés pour compléter cette notion de
distance entre deux solutions :
- P2 : L'écart type des valeurs des variables entre les deux
solutions.
- P3 : Le nombre d'objets modifiés.
- P4 : Le nombre d'objets modifiés, pondéré par le type de
ces objets. Ce paramètre permet de préférer par exemple des solutions
dans lesquelles le changement de durée est effectué sur un texte ou une
image plutôt que sur une vidéo ou sur un objet sonore. En effet, on
préférera conserver la qualité optimum d'une vidéo ou d'un son.
Finalement la fonction de distance est une combinaison de tous ces paramètres,
ce qui signifie que la fonction de distance Fd est définie comme
suit :
Fd (S1, S2) = aP1 + bP2 + cP3 + dP4
où a, b, c et d sont les poids associés aux paramètres tels que a + b + c +
d = 1.
Cette fonction peut être ajustée (en changeant les valeurs de a, b, c et d)
pour satisfaire les besoins de l'environnement auteur. Cette définition est
suffisamment générale pour être adaptée au choix de l'auteur ou au contexte
d'édition. Nous avons pu le vérifier par exemple dans l'éditeur de Workflow
(Chapitre VI, section 3).
Nous allons voir à présent comment orienter la recherche de solution de
deux manières différentes.
5.3.2 Utilisation des contraintes
hiérarchiques
L'idée de base des contraintes hiérarchiques [Borning92] est d'associer un
poids aux contraintes. Lorsque le résolveur de contraintes ne peut satisfaire
deux contraintes qui sont en opposition, il satisfait celle de poids le plus
fort.
L'utilisation de contraintes hiérarchiques permet entre autres, d'orienter
la recherche de solutions. Pour cela, on insert en plus des contraintes du
problème initial (de poids le plus fort possible), des contraintes de poids
plus faible qui serviront à exprimer un ensemble de préférences.
Par exemple, dans l'exemple de la Figure V-5, la spécification permet
d'indiquer au résolveur ce qu'il doit modifier en priorité lors d'une
résolution.
| x=4 poids
= Fort
y=3 poids =
Faible
x=y poids = Très
Fort
|
Figure V-5 : Exemple de spécification utilisant des contraintes
hiérarchiques
Aujourd'hui, la plupart des résolveurs utilisés dans Kaomi permettent de
définir de tels poids sur les contraintes (Deltablue, Cassowary). Ces
contraintes peuvent être utilisées par le système auteur pour donner des
informations externes aux résolveurs de contraintes, comme la durée optimum
des médias qu'il faut chercher à conserver. Chaque étape d'édition nécessite
de ce fait non seulement un ajout/retrait de variables et/ou de contraintes
relatives à l'action d'édition de l'auteur, mais aussi une phase de gestion de
cet ensemble de contraintes additionnelles.
5.3.3 Utilisation d'heuristiques
Les mécanismes de résolution de contraintes possèdent en général les deux
étapes suivantes :
- choix d'une variable à évaluer ;
- choix d'une valeur pour la variable choisie.
Le système peut définir des heuristiques pour orienter le choix de la variable
et/ou le choix de la valeur pour la variable.
Par exemple, dans la première étape une fonction peut trier les variables à
évaluer en fonction du type des objets (texte, son, vidéo,..), et du nombre de
relations que les objets ont directement ou indirectement. La seconde étape
peut utiliser une fonction pour permettre de choisir les valeurs des variables
en fonction de leur valeur courante et des valeurs Min et Max de
l'intervalle.
Cette technique est utilisée par exemple dans Jsolver [HonWai99].
6. Les différentes approches existantes pour le
calcul de solution
Nous avons choisi de présenter les résolveurs en fonction du mécanisme de
résolution qu'ils proposent. Nous présenterons dans la section 6.1 les
méthodes de résolution locales, et dans la section 6.2 les méthodes de
résolution globales. Dans une troisième partie (section 6.3) nous présenterons
un algorithme basé sur le simplex. Enfin, dans une dernière partie nous
présenterons des algorithmes spécialisés que nous avons développés pour la
résolution de sous problèmes dans le cadre de l'édition et la présentation de
document (section 6.4).
6.1 Les approches locales
Les résolveurs locaux ont pour objectif d'utiliser la connaissance de
l'ensemble des contraintes et des dépendances entre elles pour optimiser le
calcul de solution après une modification.
Pour cela, ils construisent dans un premier temps un graphe de contraintes
(Figure V-6). Chaque variable du problème est représentée par un cercle,
chaque contrainte est représentée par un carré, et chaque arc représente
l'appartenance d'une variable à une contrainte.
Dans un deuxième temps, à chaque contrainte est associée un ensemble de
méthodes qui explicitent comment répercuter la modification d'une variable sur
les autres variables présentes dans la contrainte. Par exemple, une méthode
associée à la contrainte C1 (Figure V-6) peut être A ¬ C - B qui indique comment répercuter une modification
de C et/ou B (ce sont les entrées de la méthode) sur A (c'est la sortie de la
méthode).
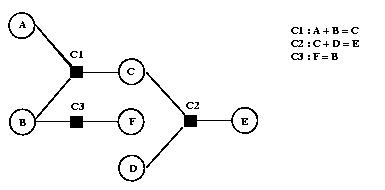
Figure V-6 : Graphe de contraintes
Une fois ces informations mises à jour, la fonction d'un résolveur local,
après une modification de la valeur d'une variable est de décider :
- Les contraintes à réévaluer : seules celles qui risquent d'être
violées par la perturbation et par ses conséquences sont
reconsidérées.
- Les méthodes de résolution à utiliser : pour chaque contrainte
à réévaluer, il faut décider quelle est la méthode associée qui va
permettre de la satisfaire à nouveau.
- L'ordre dans lequel celles-ci doivent être appliquées afin de
satisfaire à nouveau l'ensemble des contraintes.
Une des méthodes utilisées pour assurer ces trois fonctionnalités est la
méthode par propagation locale de valeur. L'idée sous-jacente à cette
technique est de dire que dès que la contrainte possède assez d'informations
pour calculer des valeurs, elle les calcule. La phase de résolution se
décompose en deux phases :
1. Une phase de planification : au cours de celle-ci le résolveur
sélectionne une méthode pour chacune des contraintes à recalculer, et
uniquement pour celles-ci. Cet ensemble de méthodes est calculé en partant
de la variable perturbée, et en identifiant toutes les contraintes
potentiellement insatisfaites.
Pour chacune de ces contraintes une méthode de résolution (parmi celles
qui sont définies) est choisie. Cette méthode doit prendre la variable
perturbée en entrée. Le système doit alors propager les modifications
liées à l'utilisation de cette méthode. L'ordre d'exécution correspond à
un tri topologique de ce graphe en fonction de son orientation.
Par exemple une orientation possible dans l'exemple de la Figure V-6
est donnée dans la Figure V-7, cette orientation répercute une
modification de A sur les variables C, D et F.
2. Une phase d'exécution pendant laquelle le plan constitué est
exécuté en séquence. Dans cette phase, les valeurs connues sont propagées
le long des arcs du graphe de contraintes.
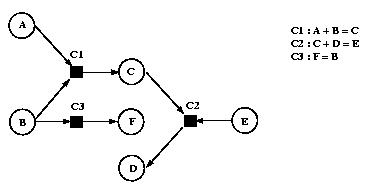
Figure V-7 : Orientation du graphe de contraintes
Les avantages de la propagation locale sont l'efficacité et la facilité de
compréhension du comportement des variables.
Dans un contexte d'édition, l'utilisation de plan est très intéressante
lors des phases de navigation et de manipulation. En effet, lorsque l'auteur
sélectionne un objet pour le déplacer le résolveur calcule un plan,
c'est-à-dire qu'il calcule un sous-ensemble du graphe de contraintes qui sera
suffisant pour répercuter les déformations lors du déplacement. Le résolveur
oriente ce sous-graphe pour propager dans le graphe la valeur modifiée par
l'auteur. Ainsi, lors de chaque déplacement élémentaire le système n'aura qu'à
utiliser le plan et propager les modifications sur les autres variables
affectées par la perturbation.
Les désavantages bien connus de ces méthodes sont :
- L'incomplétude de la méthode, c'est-à-dire que le système peut
ne pas trouver de solution alors qu'il en existe une. Cela est lié par
exemple à une orientation du graphe vers une valuation des variables
sans solution.
- L'impossibilité de supporter des cycles dans le graphe de
contraintes. Par conséquent de tels systèmes rejettent les systèmes
de contraintes qui introduisent des cycles. Dans notre contexte, les
systèmes de contraintes que l'on manipule engendrent des graphes de
contraintes fortement cycliques. Des travaux ont été réalisés pour
supporter des graphes cycliques. Dans Skyblue [Sannella95] par exemple,
le traitement des cycles est déféré vers un résolveur spécialisé.
Cependant ces techniques ne semblent pas adaptées aux graphes fortement
cycliques du fait que toute la résolution du problème est déférée au
résolveur spécifique, et de ce fait on ne tire plus profit de la méthode
locale. Dans notre contexte, dès d'un objet appartient à un groupe
d'objets, nous avons un cycle.
- La manipulation de contraintes uniquement fonctionnelles. Une
contrainte à n variables est fonctionnelle, si lorsque l'on fixe n-1
variables, la dernière est déterminée de façon unique. Dans notre
contexte, les contraintes qui limitent l'intervalle de validité d'une
variable ne sont pas fonctionnelles.
- L'absence de remise en cause du plan calculé au début d'une
opération d'édition lors d'une succession d'opérations d'édition
identiques. Par exemple, tout au long du déplacement d'un objet dans la
vue de présentation ce seront les mêmes déformations qui seront
appliquées (Figure V-8). Si nous avons trois objets A, B et C placés les
uns à côté des autres, et que nous déplaçons l'objet A vers la droite,
on aimerait, dans un premier temps, retailler B, et dans un deuxième
temps C, ou alors de répartir la déformation de manière équivalente sur
les deux. Dans le cas d'un résolveur local, on aura B qui prendra la
taille minimale autorisée par les contraintes, et après tout déplacement
sera impossible. Il faudra recalculer un nouveau plan et ajouter une
nouvelle contrainte pour dire que B n'est plus modifiable, et ainsi
forcer le résolveur à déformer C. Pour éviter cela, il faut donc changer
le plan à chaque fois que cela est nécessaire. Le résolveur devrait
permettre de changer localement le plan de manière intrinsèque.
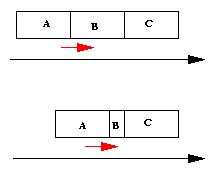
Figure V-8 : Absence de remise en cause du plan
Malgré ces limitations les techniques employées, comme la définition de
poids associés aux contraintes, pour contrôler la solution et orienter la
recherche sont intéressantes et adaptables à notre problème. Le résolveur
Deltablue ([Sannela93]) est une implémentation de résolveur local utilisant
des poids.
On peut noter que cette technique de résolution est la plus employée dans
les applications graphiques. De nombreux travaux ont été faits sur le sujet et
se poursuivent (ex : ThingLab [Maloney89] et SketchPad [Crilly95]).
Les résolveurs basés sur les approches locales sont intéressants du fait
qu'ils ne manipulent pas à chaque étape l'ensemble du réseau de contraintes,
mais seulement le sous-ensemble nécessaire.
Cependant, dans un contexte d'édition, ces méthodes sont trop limitatives
pour être utilisées telles quelles, sans mettre en place un contrôle fin des
résolveurs. En effet, l'impossibilité de manipuler des cycles dans le graphe
de contraintes et l'absence de remise en cause du plan sont des inconvénients
majeurs dans un contexte d'édition.
Néanmoins, les performances de résolution méritent qu'on étudie ces
résolveurs, non pas pour les utiliser de manière globale dans l'application,
mais ponctuellement pour la résolution de problèmes nécessitant de hautes
performances temporelles.
6.2 Les approches globales
Nous venons de voir que les méthodes locales ne permettent pas de répondre
complètement à nos besoins spécifiques. Nous étudions à présent l'autre type
d'approche, les approches globales. Ces approches parcourent toutes les
valeurs possibles de toutes les variables jusqu'à trouver une solution (quand
elle existe.) Il existe de nombreux algorithmes [Verfaillie95] qui utilisent
cette approche et qui se différencient de part leur manière de parcourir
l'ensemble des valeurs. On ne présentera qu'un seul algorithme de cette classe
qui est représentatif de l'approche. Cet algorithme, basé sur une technique de
backtrack est utilisé dans les problèmes de satisfaction de contraintes. Il
est présenté ci-dessous.
6.2.1 L'algorithme de backtrack
Nous rappelons simplement les caractéristiques essentielles de cet algorithme.
Dans l'état initial, aucune variable n'est affectée. À une étape donnée,
l'ensemble des variables est divisé en deux groupes, les variables affectées
et les variables non affectées. La solution donnée par les variables affectées
est cohérente par rapport aux sous-ensembles de contraintes qui ne portent que
sur ces variables. L'étape va consister à affecter une nouvelle variable, le
système choisit une variable et une valeur dans l'ensemble de celles qui sont
possibles, et vérifie la cohérence. Si le système est cohérent, il passe à
l'étape suivante, si le système est incohérent, il essaie une autre valeur
pour la variable considérée. Si toutes les valeurs ont été considérées, il
désaffecte une des variables affectées, et repart à l'étape n-1.
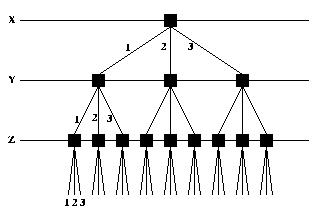
Figure V-9 : Arbre de recherche
Dans l'exemple de la Figure V-9, on peut voir un arbre de recherche
possible dans le cas où nous aurions des contraintes qui portent sur trois
variables X, Y et Z (chacune étant définie dans l'intervalle [1..3]). Le
système dans un premier temps évaluera X, en lui affectant par exemple la
valeur 1, dans un deuxième temps il évaluera Y puis Z. Si cette évaluation ne
satisfait pas le système de contraintes, il choisira une nouvelle valeur pour
Z. Si aucune des valeurs de Z ne permet de satisfaire l'ensemble de
contraintes, le système choisira une nouvelle valeur pour Y, et ainsi de
suite.
C'est la méthode de résolution employée dans IlogSolver [IlogSolver00].
Des heuristiques sur le choix des variables à remettre en cause lors de
retour arrière ou sur le choix des valeurs pour une variable sont réalisables,
ce qui permet d'améliorer et de personnaliser cet algorithme de manière à
orienter la recherche de solutions. Par exemple, on peut imaginer, dans notre
cas, de désaffecter en priorité les variables représentant les instants de
début et fin des délais.
L'avantage majeur de cette technique est sa complétude : on trouve toujours
la solution si elle existe et la possibilité pour l'utilisateur de contrôler
la recherche de solution en cas de réponses multiples.
Ses inconvénients sont :
- l'obligation de travailler sur des domaines finis, or nos systèmes de
contraintes manipulent des domaines infinis ;
- le coût généralement très grand de cette technique, qui procède par
énumération, lorsque le domaine des variables est trop grand.
Cependant ces deux inconvénients peuvent être réduits par la remarque suivante
: il est possible d'utiliser sur nos problèmes des algorithmes de filtrages
pour réduire les domaines de validité de toutes les variables aux valeurs qui
apparaissent dans au moins une solution du système de contraintes, et donc de
diminuer l'espace de recherche améliorant ainsi les coûts d'un algorithme de
type backtrack. Un autre avantage de l'utilisation d'un algorithme de
filtrage, est que celui-ci permet de connaître l'intervalle de validité des
variables.
Il existe de nombreux travaux pour améliorer ce mécanisme de résolution en
intégrant par exemple la connaissance d'une résolution précédente pour
améliorer la résolution courante. Ces mécanismes sont très intéressants dans
un contexte d'édition incrémentale. Ces travaux sont résumés et les différents
algorithmes présentés dans [Verfaillie95].
6.2.2 jSolver : un implémentation basée sur le
backtrack
Nous allons illustrer ces approches par la présentation du résolveur jSolver
[HonWai99]. jSolver est une librairie Java qui permet de manipuler et de
résoudre des CSP. Chaque variable est définie dans un domaine entier fini.
L'algorithme de recherche se décompose en quatre étapes (Figure V-10):
- Choisir une variable dans l'ensemble des variables à évaluer.
- Choisir une valeur pour la variable dans le domaine, s'il n'y a plus de
valeur possible un retour arrière intervient.
- Affectation de la valeur à la variable.
- Propagation des contraintes.
L'implémentation de jSolver nous a permis de définir différentes stratégies
pour les étapes 1 et 2. En effet, jSolver permet d'ordonner les variables à
évaluer ainsi que les domaines de définition des variables. On peut ainsi
prendre en compte plus facilement des préférences de l'auteur vis-à-vis des
déformations (minimisation du nombre d'objets déformés, localité des
déformations, ).
Outre ces fonctionnalités très intéressantes dans notre contexte d'édition,
jSolver offre un mécanisme de planification à la Deltablue (section 6.1). Ce
mécanisme, bien contrôlé, peut être très utile pour certaines opérations
d'édition répétitives. On peut noter que par rapport à Deltablue, jSolver est
complet. C'est-à-dire que s'il existe une solution, il la trouve.
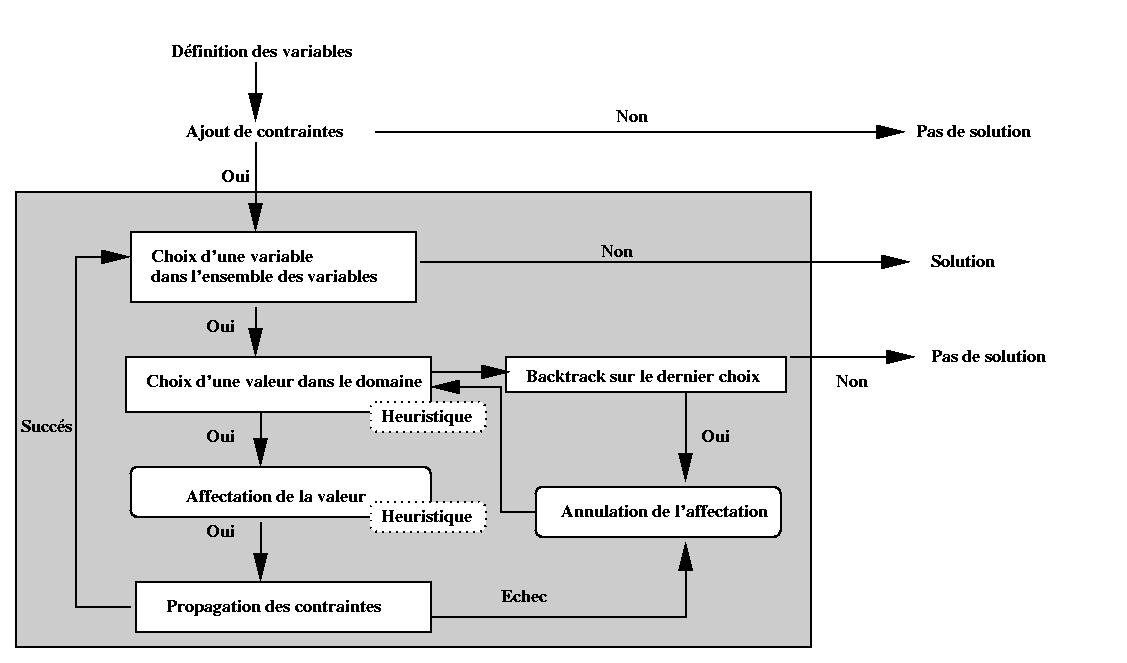
Figure V-10 : jSolver
6.3 Les approches basées sur l'algorithme du
simplex
De nombreux travaux ont permis de résoudre des problèmes linéaires. Le premier
algorithme permettant de les résoudre est le simplex réalisé par Dantzig dans
les années 40 [Dantzig49]. De nombreuses variantes ont été réalisées de
manière à améliorer les performances temporelles de la résolution et dans un
deuxième temps de définir une fonction d'optimisation (f). La
résolution de l'algorithme devra maximiser la valeur de cette fonction tout en
satisfaisant l'ensemble de contraintes. Les algorithmes que nous allons
présenter par la suite sont basés sur le Dual-simplex [Dantzig54, Marriott98].
6.3.1 Cassowary
Cassowary est un résolveur de contraintes qui traite des équations et des
inéquations linéaires. Cet algorithme a été développé à l'université de
Washington par Badros et Borning ([Badros98]).
L'algorithme se décompose en deux phases :
- Phase de prétraitement : cette phase vise à traduire le problème
sous une forme ne contenant ni inégalité, ni variable négative, de manière
à résoudre l'ensemble de contraintes obtenu par le simplex.
- Les inégalités de la forme x ³ y sont
traduites sous la forme x = a + y.
- Les variables négatives (v), sont substituées par des équations
de la forme e = -v, on substitue ensuite toutes les
occurrences de v par -e. La résolution des variables
v, se fera dans une étape postérieure, une fois la valeur de
e connue.
- Optimisation pour le simplex : les contraintes sont mises sous
forme de matrice. Une optimisation de la matrice est réalisée dans le but
de favoriser la recherche d'une solution optimale et de limiter le nombre
de variables manipulées par le simplex. Cette optimisation se base en
partie sur les poids associés aux contraintes. Ce mécanisme complexe est
présenté complètement dans [Badros98].
- Une solution est ensuite obtenue par la méthode du simplex.
Les travaux réalisés ont aussi eu pour but de rendre incrémentales les
opérations d'ajout et de retrait de contraintes. Ces travaux sont rendus
complexes par l'optimisation des données pour le simplex. En effet, il est
nécessaire lors de l'ajout et du retrait d'équation de maintenir une cohérence
entre le problème initial est sa version optimisée.
6.3.2 QOCA
QOCA [Marriott98b] est une boîte à outils pour résoudre les CSP qui est
construite au-dessus de Cassowary. QOCA utilise Cassowary pour résoudre les
contraintes et introduit des notions supplémentaires pour contrôler la
solution trouvée par le résolveur.
Cette boîte à outils est basée sur un modèle de normalisation de l'espace
de solution. Cette normalisation, permet de :
- définir une mesure qui donne la distance entre deux affectations d'une
même variable (dans des solutions différentes). Cette mesure est proche
du paramètre P2 de la fonction de distance que nous avons
défini (section 5.3.1).
- définir une mesure de distance entre deux solutions de l'ensemble de
contraintes, à partir de la mesure de la distance entre deux
affectations de variables.
La difficulté consiste à maintenir la normalisation de l'espace lors
d'opérations modifiant le système de contraintes, ces opérations sont :
- Ajout de contraintes au jeu de contraintes courant, dans ce cas,
l'affectation des variables est celle qui est la plus proche possible de
la solution courante. La notion de plus proche est définie grâce à la
métrique de l'espace.
- Retrait d'une contrainte, dans ce cas, la solution courante reste
inchangée.
- Modification de ma solution courante, dans ce cas l'auteur peut
suggérer un ensemble de valeurs pour les variables, et le système
choisit la nouvelle solution de manière à ce que celle-ci soit la plus
proche possible de celle suggérée.
La boîte à outils a été utilisée avec des outils comme Idraw [Helm95], et
donne des résultats très satisfaisants. Cependant, dans notre contexte, cette
approche présente quelques limites. Par exemple, le fait de ne pas réévaluer
le système de contraintes lors du retrait d'une contrainte pose des problèmes
lors de l'utilisation des domaines de validité. En effet dans notre contexte,
lors du retrait d'une contrainte, l'intervalle de validité des variables doit
être recalculé.
6.4 Résolveurs spécifiques développés dans
Kaomi
Pour tirer profit de la structure interne de Kaomi qui comporte un graphe
temporel (voir chapitre IV), deux algorithmes spécifiques ont été implémentés
dans le projet. Le premier est une adaptation de PC2 (section 6.4.1) pour
vérifier la cohérence temporelle et formater une hiérarchie de graphes
(réalisé par F. Bes [Bes98]). Le second, que j'ai réalisé, est un algorithme
permettant à l'auteur d'effectuer des modifications dans la vue temporelle,
pour déplacer et retailler les objets dans cette vue ([Tardif97]).
6.4.1 PC2 adapté
L'ensemble des contraintes temporelles peut être directement traduit dans un
graphe temporel orienté et acyclique si l'on reste dans le cadre des STP
(Simple Temporal Problem). La notion de STP, qui est une restriction des CSP a
été introduite par Dechter ([Dechter91]). Un STP est un ensemble de
contraintes où toutes les variables représentent des instants temporels et
toutes les contraintes s'expriment sous la forme de différences bornées. De ce
fait, il ne peut supporter les relations de causalité. Dans le chapitre IV
(section 6.3) nous avons présenté la construction du graphe correspondant. Les
noeuds sont les instants de début et de fin des intervalles. La présence d'un
arc entre deux noeuds n1 et n2, traduit le fait que
n2 se situe temporellement après n1. Les arcs sont
étiquetés par trois valeurs :
- La durée prévue de l'objet.
- La borne inférieure de l'intervalle de flexibilité de l'objet dans le
scénario.
- La borne supérieure de l'intervalle de flexibilité de l'objet dans le
scénario.
Dans l'exemple de la Figure V-11, on a trois objets A, B, C. Ces trois objets
ont des durées respectives de : A[1,2,4], B[3,5,9], C[2,3,5]. Il y a trois
relations entre ces objets : Starts (A, B), Meets(A, C),
Finishes(C, B).
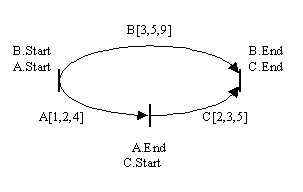
Figure V-11: Un graphe temporel
Pour vérifier la cohérence de graphes de contraintes, de nombreux
algorithmes ont été proposés. On peut citer AC3 ([Mackworth77]), AC4
([Mohr86]), DPC ([Dechter88]) ou AC6 ([Bessière94]). Ces algorithmes sont
basés sur la notion de cohérence d'arcs ou de cohérence de chemins. PC2
[Mackworth77] est un algorithme basé sur la cohérence de chemins qui filtre
les intervalles de durée associés aux arcs de manière à supprimer les valeurs
qui n'appartiennent à aucune solution.
PC2 adapté au graphe temporel
Une adaptation de PC2 a été utilisée par Dechter ([Dechter91], [Dechter88])
pour vérifier la cohérence de graphes temporels.
PC2 se base sur un graphe temporel complet, et considère tous les chemins
de longueur inférieure ou égale à deux entre deux noeuds, pour filtrer les
valeurs qui n'appartiennent à aucune solution. Un état incohérent est détecté
quand toutes les valeurs d'un intervalle ont été éliminées.
L'algorithme peut être décrit comme suit :
- Complétion du graphe, jusqu'à obtenir un graphe complet. Cette étape
permet de rendre possible le calcul de tous les chemins de longueur
inférieure ou égale à deux entre 2 noeuds. Les arcs introduits ont une
durée initiale de [-¥ , +¥ ].
- Pour chaque couple de noeuds :
- La durée de chaque chemin de longueur inférieure ou égale à deux est
calculée.
- L'intersection de ces durées est comparée avec la durée de l'arc reliant
ces deux noeuds.
- Si cette intersection est vide, une incohérence est détectée, sinon la
valeur de l'intersection est prise comme nouvelle durée de l'arc entre les
deux noeuds.
L'étape 2 est répétée jusqu'à l'obtention d'une stabilité des durées des arcs
du graphe.
Le résultat de cet algorithme est un graphe minimal pour le jeu de
contraintes donné. Les intervalles sur les arcs représentent les intervalles
de validité des variables de durée. C'est-à-dire que si l'on choisit une
valeur dans un des intervalles, alors cette valeur appartient à une solution.
On peut donc trouver une valuation pour toutes les durées des autres arcs.
Un formateur basé sur PC2 [Bes98, Layaïda97]
Cette propriété nous permet d'utiliser PC2 comme formateur, en faisant une
succession de filtrages et d'affectations.
Dans une approche telle que PC2 l'ajout de contraintes est relativement
simple grâce à la construction du graphe, cependant, le retrait d'une
contrainte est beaucoup plus difficile du fait que les domaines ont été
filtrés. Il faut donc réintroduire ces domaines. L'implémentation de PC2 dont
nous disposons à l'heure actuelle oblige, lors de chaque retrait de
contrainte, à réintroduire les domaines non filtrés et à filtrer le graphe. On
peut noter que des méthodes pour permettre de réduire les réintroductions de
valeurs dans les domaines ont été étudiées et évaluées principalement sur AC3
et AC4 ([Bessière91]) et pourraient être implémentées dans PC2.
Adaptation de PC2 pour une hiérarchie de graphes (HPC2) [Bes98]
Avec la définition d'une hiérarchie d'objets temporels, la dimension
temporelle d'un document ne se représente pas par un graphe mais par une
hiérarchie de graphes. Un arc dans un graphe à un niveau donné représente un
objet ou un graphe du niveau inférieur. La propagation d'une contrainte se
fait dans un premier temps au niveau du graphe dans laquelle elle a été
introduite, et ensuite elle est propagée dans les niveaux supérieurs et
inférieurs jusqu'à obtenir une stabilité de la hiérarchie de graphe.
Dans la Figure V-12 je présente l'algorithme HPC2 ([Bes98]) proposé pour
manipuler de telles hiérarchies.
Cet algorithme tire profit des domaines minimaux calculés par PC2 pour
réduire la propagation entre les graphes.
Nous allons présenter deux versions qui sont utilisées dans Kaomi :
- La première incrémentale, qui permet de vérifier la cohérence à chaque
insertion de relation en tirant profit du formatage à l'étape
précédente. Dans ce cas, il faut vérifier la cohérence au niveau où la
contrainte a été insérée (ligne 10), il faut ensuite faire une
propagation dans tous les sous-graphes (ligne11), et ensuite remonter
cette valeur sur le composite englobant (ligne 12). Cette version de
l'algorithme est utilisée pour les opérations d'édition (ajout) de
l'auteur. Elle n'est pas utilisée pour le retrait d'objet à cause des
limitations de la version courante de PC2.
- La deuxième non incrémentale, permet de vérifier la cohérence d'un
graphe quelconque. Dans ce cas, il faut vérifier la cohérence d'abord
dans les arbres les plus bas dans la hiérarchie (ligne 5), et ensuite
faire propager les valeurs remontées entre frères (ligne 7). Cette
version de l'algorithme est utilisée après la phase de lecture du
fichier source. En effet, dans le contexte d'ouverture du document, nous
appelons le mécanisme de résolution à la fin de la construction du
graphe, et de ce fait, cela a nécessité une adaptation de l'algorithme à
cette utilisation spécifique.
- HPC2_incremental(Graphe G) {
- Vérifier_cohérence(G);
- }
- HPC2_global(Graphe G) {
- Reduire_BottomUpFirst(G);
- Pour chaque G1
ÎW (G)
- Reduire_TopDown(G1);
- }
- Vérifier_Cohérence (Graphe G)
- PC2(G);
- Pour chaque G1
ÎW (G)
- Reduire_TopDown(G1)
- Vérifier_Cohérence(Parent(G))
- }
|
- Reduire_BottomUpFirst(Graphe G)
- Pour chaque
G1 Î W (G)
- ReduceBottomUpFirst(G1)
- PC2(G1)
- }
- Reduire_TopDown(Graphe G) {
- PC2(G)
- Pour chaque
G1 Î W (G)
- Reduire_TopDown(G1)
- }
W (G)= {Graphes
représentés par un arc dans G pour lesquels la durée a été
modifiée}
|
Figure V-12 : Algorithmes HPC2
6.4.2 Navigation dans la vue temporelle :
l'algorithme AVT
La vue temporelle de Kaomi, comme nous l'avons présentée dans le chapitre
précédent, offre une visualisation du scénario temporel du document, elle
permet donc d'afficher une solution du réseau de contraintes. De plus, cette
vue permet à l'auteur de naviguer dans l'espace de solutions. Lors de mon
projet de DEA, j'ai défini un algorithme qui prend en charge cette tâche de
navigation. Nous l'appellerons par la suite AVT (Algorithme de la Vue
Temporelle).
L'objectif de l'AVT est de calculer le plus rapidement possible une
nouvelle solution à chaque action de l'auteur dans la vue temporelle. Cet
algorithme est donc complètement spécialisé pour arriver à cet objectif.
L'algorithme réalisé nécessite la connaissance des intervalles minimaux sur
les arcs du graphe. Il est donc nécessaire avant d'appliquer l'algorithme de
la vue temporelle qu'un autre algorithme du type PC2 calcule les domaines
minimaux. Avec cette hypothèse, on peut assurer que si l'auteur choisit une
des valeurs d'un des domaines minimaux, alors il existe une solution au
système de contraintes.
L'AVT est basé sur le graphe temporel résultant de la spécification de
l'auteur et non pas sur le graphe de contraintes. Cet algorithme est présenté
complètement dans [Tardif97], je ne rappelle ici que son principe. La méthode
utilisée est une propagation de la modification vers les intervalles les plus
proches capables d'absorber cette modification. C'est un algorithme en deux
étapes :
- Collecte d'information : en fonction du jeu de contraintes et de
l'action de l'auteur (telle que déplacement ou retaillage d'un objet), le
résolveur calcule l'intervalle maximal pour le déplacement (ou le
retaillage) de cet objet. Il calcule aussi les objets qui seront affectés
(déplacés ou retaillés) par cette modification.
- Propagation de l'action de l'auteur : chaque fois que l'auteur fait une
action élémentaire (par exemple à chaque étape d'un déplacement), le
système utilise les informations calculées à l'étape précédente pour
appliquer les déformations. On peut comparer cette approche avec
l'utilisation des plans dans Deltablue.
6.5 Bilan des approches
L'étude bibliographique de cette section des différentes méthodes de
résolution nous amène a des conclusions générales sur l'utilisation des
résolveurs de contraintes.
Les algorithmes globaux présentés semblent pouvoir répondre complètement à
nos besoins d'expressivité. Cependant les performances temporelles de tels
algorithmes restreignent leur utilisation.
Les algorithmes locaux qui ont la réputation d'être très performants sont
par contre incomplets et ne peuvent être utilisés que partiellement pour
répondre à notre problème.
Enfin, les algorithmes à base de simplex semblent offrir le meilleur
compromis entre expressivité et rapidité.
Cette première analyse doit être et sera complétée par une analyse
quantitative et qualitative dans un contexte d'édition (section 8).
Nous allons maintenant dans un premier temps, expliquer comment
s'inscrivent les résolveurs de contraintes dans la boîte à outils Kaomi
(section 7), nous présenterons ensuite l'évaluation des différents résolveurs
dans leur contexte d'utilisation (section 8), et nous conclurons ce chapitre
en faisant un bilan des différentes utilisations possibles d'une technologie à
base de contraintes dans un contexte d'édition de documents multimédias.
7 Le module contraintes de Kaomi
Le module de contraintes de Kaomi a été implémenté comme un service de la
boîte à outils et n'a donc de ce fait pas été intégré directement dans chacun
des modules utilisant un résolveur de contraintes (vue temporelle, vue
d'exécution, module d'édition) (Chapitre IV section 5.2).
Cela a été réalisé pour deux raisons :
- Permettre une grande souplesse dans le remplacement des résolveurs et
l'intégration de nouveaux résolveurs. Cela nous a permis de tester
facilement les différents résolveurs dans les différents contextes
d'utilisation.
- Changer de résolveurs en fonction du type de manipulation ou de
besoins que l'on a. C'est-à-dire que nous disposons d'un module, qui à
partir de certaines informations (type d'utilisation, type de données)
nous permet d'appeler un résolveur, sans pour autant savoir lequel on
utilise réellement à un instant t. Cela permet, par exemple, d'utiliser
un résolveur différent lors de l'ajout d'une relation et lors d'une
manipulation dans la vue temporelle où les besoins en termes de
performances temporelles sont plus importants.
Au cours de cette section nous présenterons dans un premier temps
l'architecture du module de contraintes (section 7.1) et plus particulièrement
l'organisation hiérarchique des résolveurs de contraintes (section 7.2). Dans
un deuxième temps nous présenterons les politiques de formatage choisies dans
Kaomi (section 7.3).
Enfin dans la section 7.4 nous présenterons comment se réalise
l'intégration d'un résolveur de contraintes dans Kaomi.
7.1 Architecture du module de
contraintes
La structure du module de gestion de contraintes est la suivante dans Kaomi :
- Un ensemble de résolveurs avec des propriétés et une structure de
données qui leur sont propres.
- Un module de choix qui permet de fournir un résolveur lorsqu'un module
désire en utiliser un.
Ce module de contraintes peut être utilisé par toute l'application. Par
exemple, à l'heure actuelle, quatre modules l'utilisent : le module de
présentation spatial dans la vue d'exécution, les modules temporels dans les
vues d'exécution et temporelle, ainsi que le module édition de Kaomi.
Le processus général d'utilisation du module contraintes est décrit dans la
Figure V-13. Ce processus est le suivant.
Lorsque l'auteur effectue une modification sur son document, par exemple,
une action d'édition (transition 1), cette opération d'édition est appliquée
dans le module d'édition. Ce module met à jour sa structure de données
(transition 2). De manière à garantir la cohérence du document et à propager
la modification de l'auteur, on fait appel au résolveur de contraintes pour
calculer l'ensemble des modifications à faire (transition 3). Le résolveur
calcule alors cet ensemble de modifications et les propage à la structure de
données du document (transition 4). Une fois la structure de données à jour,
celle-ci indique au module d'édition que le calcul est terminé (transition 5),
et ce dernier peut demander la mise à jour de l'affichage (transition 6).
Dans le cas d'une modification locale à une vue, le processus est
similaire. Les modifications se font localement sur les structures de données
de la vue. Le processus met alors en oeuvre les transitions 7 à 12.
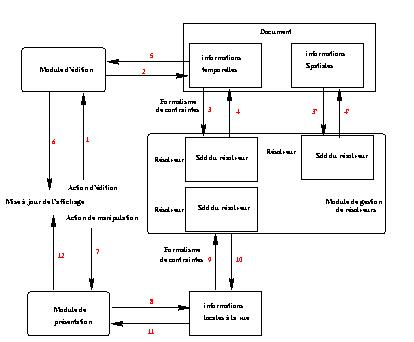
Figure V-13 : Maintiens des relations lors de l'édition
7.2 Organisation hiérarchique des
résolveurs
Dans le cadre d'une décomposition hiérarchique du document, on utilise un
résolveur par niveau de hiérarchie, et on utilise un algorithme qui utilise le
même principe de propagation hiérarchique que celui présenté dans HPC2 (voir
chapitre V) pour propager les valeurs entre les différents niveaux de
hiérarchie. Dans l'exemple de la Figure V-14, on peut voir une hiérarchie
temporelle avec les différentes instances de résolveurs.
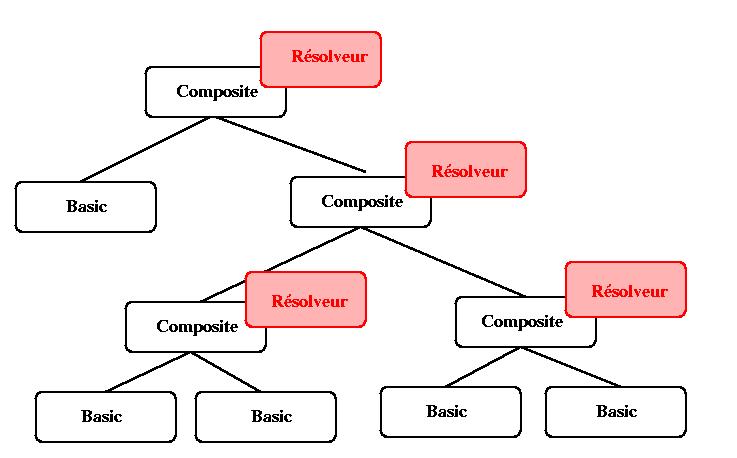
Figure V-14 : Hiérarchie de résolveurs
Nous rappelons qu'à chaque étape, l'hypothèse est : les domaines de
validités sur les intervalles de valeurs associés aux objets sont
maintenus.
Lors d'une modification de valeur le résolveur hiérarchique s'occupe de
limiter les propagations seulement aux résolveurs pour lesquels c'est
nécessaire. Par exemple, dans la Figure V-15, nous illustrons deux situations
:
- Dans le premier cas, l'auteur a modifié une valeur sur un objet de
base, cette modification n'a pas remis en cause les domaines minimaux du
composite, de ce fait, cette opération n'a nécessité qu'un seul
formatage.
- Dans le deuxième cas, l'auteur modifie la valeur d'un des attributs
d'un objet de base, le résolveur du composite supérieur calcule une
nouvelle solution. Si ce calcul modifie l'intervalle minimal du
composite, l'information est propagée vers le composite supérieur. Dans
le cas où l'intervalle minimal n'est pas modifié, l'information n'est
pas propagée vers le composite ascendant. Dans les deux cas, le nouveau
formatage est propagé à tous les descendants. Si un des descendants est
un composite, alors cela nécessite une phase de formatage. Cette phase
de formatage, du fait du maintien des domaines minimaux ne nécessitera
pas une remise en cause des formatages de niveaux supérieurs déjà
effectués.
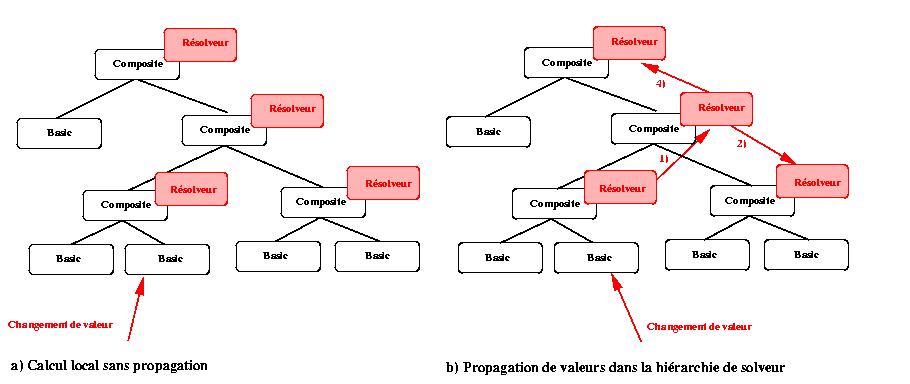
Figure V-15 : Propagation des valeurs
On peut voir qu'un des avantages de cette structuration est de limiter les
calculs des résolveurs de contraintes.
On peut noter que des langages comme SMIL2 ou MHML permettent de définir
des événements entre tous les objets d'un document, et plus particulièrement
entre deux objets qui ne sont pas initialement dans le même composite
temporel. Le système doit alors recalculer une nouvelle décomposition
hiérarchique en fonction des relations contenues dans le document, telles que,
si deux objets ont une relation, ou un événement entre eux, ils sont dans le
même composite. Dans des cas extrêmes, on obtient à la fin de ce processus un
seul composite avec tous les objets du document à l'intérieur.
7.3 Politique de
formatage : compromis dans l'utilisation des résolveurs de
contraintes
De par les différentes expériences d'utilisation de résolveurs de contraintes
qui ont été faites dans le cadre de l'édition de documents multimédias
([Carcone97b], [Badros98]), nous savons que tous les besoins ne peuvent être
satisfaits par le même résolveur. On doit donc définir un certain nombre de
compromis. Nous allons décrire un ensemble qui va nous servir à restreindre
notre problème, et les expliquer en fonction des objectifs que l'on souhaite
atteindre.
7.3.1 Choix entre performances en temps de calcul et
pertinence de la solution
Le besoin essentiel, dans un environnement auteur, est de trouver rapidement
la meilleure solution du réseau de contraintes. On sait que ce problème est
complexe. De manière à réduire les temps de calcul, on peut manipuler une
définition relâchée de la meilleure solution, et se contenter de chercher une
bonne solution qui ne sera pas forcément la meilleure.
Cette solution peut être calculée en utilisant des fonctions heuristiques
dans les approches globales (jSolver), ou en orientant l'évaluation dans les
techniques locales (Deltablue).
Par exemple, dans le cas où l'on a trois objets A, B, C, avec les relations
A Before B et B before
C ( Figure V-16A). Si l'auteur décide de retailler l'objet B par la droite. Le
système a plusieurs manières de calculer une nouvelle solution, il peut par
exemple :
- réduire le délai d2 (Figure V-16B) ;
- réduire la durée de l'objet C si celui-ci est flexible (Figure V-16C)
;
- réduire le délai d1 (Figure V-16D) ;
- réduire l'objet A si celui-ci est flexible (Figure V-16E).
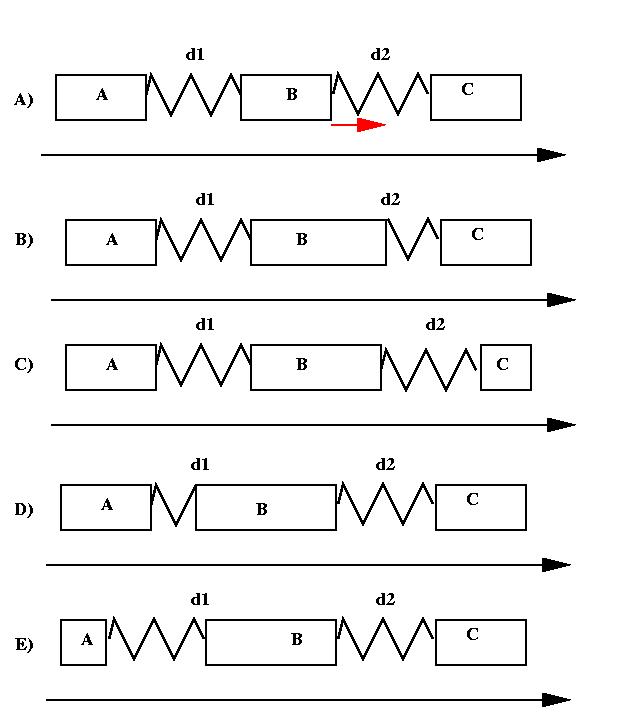
Figure V-16 : Solutions multiples
La meilleure solution dépend en partie de la manière dont l'auteur a
spécifié ses relations. Par exemple, s'il a explicitement spécifié les durées
d1 et d2, alors une bonne solution ne modifiera pas ces deux durées.
Si dans un contexte donné, la meilleure solution est la solution B, alors,
le fait de ne pas insérer de contraintes pour orienter la recherche de
solution vers cette solution a pour effet de diminuer sensiblement le nombre
de contraintes introduites dans le résolveur. La recherche de solution sera
d'autant plus rapide. Cependant, on risquera de tomber sur des solutions moins
bonnes. Toute la difficulté consiste donc à trouver un bon compromis.
7.3.2 Choix entre temps de calcul et possibilités
d'édition par des manipulations directes
Une des manières d'obtenir de bonnes performances temporelles, lors de la
résolution d'un système de contraintes, est d'introduire des restrictions dans
les opérations que l'on permet à l'auteur de réaliser. Par exemple, dans la
dimension spatiale, un des gains les plus significatifs en temps est obtenu en
interdisant à l'auteur de modifier la taille d'un objet composite, par
manipulation d'un de ses fils. De ce fait, les modifications peuvent se faire
localement, et ne remettent pas en cause la formatage de tout le document.
Si l'auteur désire modifier la taille d'un objet composite, il peut
toujours la modifier en sélectionnant directement l'objet composite ou en
modifiant un de ces frères dans la structure spatiale.
Le petit exemple est présenté dans la Figure V-17 pour illustrer une telle
limitation : l'auteur ne peut déplacer l'objet B verticalement du fait qu'il
définit la boîte englobante minimale de l'objet composite. Cependant, l'auteur
peut le déplacer horizontalement. Pour la même raison, il peut déplacer
l'objet C verticalement mais pas horizontalement. L'objet D, lui, ne peut pas
bouger car il définit deux des côtés de la boîte englobante minimale. Dans cet
exemple, la boîte englobante minimale est définie de manière dynamique par les
objets qu'elle contient.
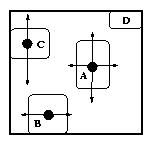
Figure V-17: Opérations d'édition spatiale sur des objets à
l'intérieur d'un composite
L'auteur peut aussi utiliser des opérations d'édition indirectes pour, par
exemple, retailler un objet composite, comme changer ses attributs Hauteur et
Largeur dans la vue attribut. L'auteur peut ainsi changer la taille des objets
composite ; on ne limite donc pas l'espace de solutions possibles de son
document.
Maintenir une boîte englobante nécessite des résolveurs capables de traiter
les cycles dans un graphe de contraintes. Maintenir la boîte englobante
minimale n'est pas une chose facile avec les résolveurs linéaires, car cela ne
s'exprime pas de manière linéaire. Il existe cependant plusieurs manières de
contourner ce problème. La première solution consiste à manipuler une
définition plus souple de la boîte englobante d'un composite : c'est-à-dire
que l'on considère une boîte englobante qui n'est pas forcément la boîte
minimale. Comme dit précédemment la seconde manière est d'interdire le
retaillage des composites.
7.3.3 Choix entre temps de calcul et pouvoir
d'expression
On peut améliorer les performances temporelles de la gestion de contraintes en
réduisant le jeu de relations que peut définir l'auteur. Par exemple, certains
résolveurs locaux sont très performants, mais ne sont pas capables de
maintenir des réseaux de contraintes cycliques. De ce fait si on désire avoir
de hautes performances, il faut supprimer les relations telles que "centrer"
ou les relations hiérarchiques qui introduisent des cycles dans le système de
contraintes.
7.3.4 Choix faits dans Kaomi
Nous avons fait dans Kaomi un choix à deux niveaux :
- Du côté du document, où nous sommes obligés d'être complet si l'on ne
veut pas trop restreindre le pouvoir d'expression, nous utilisons des
résolveurs complets.
- Dans la vue temporelle et dans la vue spatiale, nous limitons l'auteur
dans les déformations autorisées par manipulations directes. On
interdit, par exemple, le retaillage implicite de composites qui est une
opération coûteuse en temps. De plus, dans la vue temporelle, par
exemple, les déformations sont limitées au voisinage proche de l'objet
manipulé.
7.4 Intégration d'un résolveur de contraintes dans
Kaomi
Pour l'instant, chaque module (module d'édition, vue temporelle, vue
d'exécution, vue spatiale) n'utilise qu'un résolveur de contraintes. Si nous
voulions utiliser plusieurs résolveurs dans le même module, de manière à
exploiter au mieux les capacités des résolveurs en fonction du contexte et de
l'opération d'édition réalisée, cela demanderait un maintien de la cohérence
des informations partagées entre les différents résolveurs.
7.4.1 Association module / résolveur
Comme nous avons pu le voir dans le chapitre précédent, chacun des résolveurs
de contraintes a des capacités et des performances qui dépendent énormément du
contexte d'utilisation. Nous verrons dans la section 8 une évaluation
qualitative et quantitative de ces performances.
Dans le cadre de Kaomi, nous avons la possibilité, lors de la création d'un
résolveur par un module, de choisir le résolveur en fonction de certains
critères. Par exemple, le module VueTemporelle, lors de son initialisation, va
demander au module de gestion de résolveurs un résolveur temporel. Le module
VueTemporelle peut préciser sa demande en indiquant s'il veut un résolveur
optimal pour l'édition ou pour la manipulation. En fonction des différentes
informations, le module de gestion de résolveurs fournira à la vue temporelle
le résolveur le plus adapté à ces besoins. Dans Kaomi, nous utilisons en
permanence plusieurs types de résolveurs (locaux, globaux, spécialisés pour
une application spécifique), chacun étant utilisé de manière à avoir des
capacités optimales.
7.4.2 Vues temporelle et vue
d'exécution
La vue d'exécution utilise directement le résultat du formatage sur le
document pour placer les objets spatialement et pour les exécuter
temporellement. Lorsque l'auteur déplace un objet dans la vue spatiale, cela
est considéré comme une opération d'édition, et on fait appel au résolveur
associé au document pour calculer une nouvelle solution.
La vue temporelle, elle, utilise en plus un résolveur pour maintenir le
placement spatial des objets dans sa vue. En cas de déplacement, la vue
temporelle fait appel à son résolveur local pour propager les déformations, et
une fois l'opération d'édition réalisée, elle propage le résultat sur le
document de référence.
8 Evaluation des résolveurs de
contraintes
Maintenant que nous avons décrit dans quelles conditions sont utilisés les
résolveurs dans Kaomi, nous allons présenter les résultats de travaux qui ont
permis d'évaluer les différents types de résolveurs dans notre contexte
d'utilisation.
8.1 Résolveurs de contraintes
évalués
Le but de cette étude n'est pas de comparer tous les résolveurs de contraintes
existants, mais d'avoir une base de comparaison entre les différentes
techniques de résolution. Le choix des résolveurs étudiés a été fait en
fonction de deux critères :
- La représentativité de l'approche.
- Le langage d'implémentation (Java) de notre boîte à outils, le langage
d'implémentation des résolveurs a été choisi de manière à simplifier
leur intégration dans la boîte à outils.
Nous avons évalué sept résolveurs différents, cinq d'entre eux ont été
développés par des universités ou des centres de recherche publics dans un
contexte général, les deux autres ont été développés de manière spécifique à
notre système.
8.1.1 Résolveurs globaux
évalués
Les trois résolveurs à base de mécanismes globaux que nous avons évalués sont
Cassowary, jSolver et Maple [Maple98].
Les deux premiers résolveurs ont été présentés dans la section 6. Nous
rappellerons brièvement leur caractéristiques.
Cassowary :
Cassowary est un résolveur de contraintes pour les expressions linéaires. Il a
déjà est utilisé pour calculer le placement spatial d'objets [Badros98], et il
sert de base à d'autres résolveurs de contraintes tels que Qoca [Marriott98].
Son pouvoir d'expression couvre nos besoins (excepté la boîte minimale
englobante), et il est possible d'orienter la recherche de solution. Nous
avons utilisé les contraintes hiérarchiques pour réaliser cette résolution. De
ces faits, il nous a semblé pertinent d'évaluer ce résolveur.
jSolver :
A la différence de Cassowary, jSolver est un résolveur énumératif,
c'est-à-dire qu'il évalue toutes les combinaisons possibles de valeurs des
variables. Cependant, il permet à l'utilisateur de définir ses propres
heuristiques pour l'orientation de la résolution. Ainsi, nous avons pu définir
une politique pour l'ordre d'évaluation des variables ainsi que sur le choix
des valeurs. Pour définir ces heuristiques, nous nous sommes basés sur les
méthodes définies dans la section 5.3.
De plus, pour améliorer ses performances, jSolver nous donne la possibilité de
calculer un plan et de le conserver pour une succession d'opérations d'édition
similaires.
De ce point de vue, et du fait qu'il représente une approche complètement
différente de Cassowary, il nous a semblé judicieux d'évaluer ce genre
d'approches, qui de plus, grâce au contrôle qu'elle offre sur la recherche de
solution semble très intéressante dans notre contexte. On peut noter cependant
qu'une des difficultés de ces approches est qu'elles manipulent explicitement
l'intervalle de chacun des objets. Par exemple, si nous avons deux objets dont
les intervalles de durée sont compris entre 9 et 10 minutes, cela laisse un
choix de 60000 valeurs possibles, car nous travaillons en millisecondes.
Maple :
Maple ([Maple98]) a une place un peu particulière dans notre analyse : il est
considéré comme un résolveur de référence. C'est-à-dire que les performances
temporelles de ce résolveur ne nous intéresseront pas. Il servira seulement à
calculer la meilleure solution. De plus, ce résolveur est non linéaire, il
nous permet donc de manipuler des concepts comme la boîte minimale englobante.
Nous l'avons aussi utilisé pour mesurer la qualité des solutions fournies par
les autres résolveurs.
8.1.2 Résolveurs locaux évalués
La seconde catégorie de résolveurs que nous allons expérimenter est celle des
résolveurs locaux. Ce type de résolveurs semble intéressant dans notre
contexte du fait des bonnes performances temporelles qui les caractérisent.
Comme représentant de cette catégorie de résolveurs nous avons choisi
d'utiliser Deltablue.
Une des difficultés avec ce genre de résolveur est leur incomplétude. Cette
incomplétude est à deux niveaux :
- Incapacité de traiter des graphes de contraintes cycliques (dès que
nous avons des relations hiérarchiques nous avons des graphes cycliques
(voir Figure V-18)). En effet, chaque objet est dans la boîte englobante
définie par son père dans la hiérarchie. À cause de cette relation, et
des relations qui lient les variables de chaque objet, nous avons
systématiquement des cycles. Dans l'exemple de la Figure V-18 on peut
voir le graphe de contraintes associé à la relation A inside B.
- Incapacité à garantir que le résolveur trouvera une solution s'il en
existe une, même pour des graphes acycliques. Par exemple, si
l'orientation du résolveur l'emmène vers une mauvaise piste.
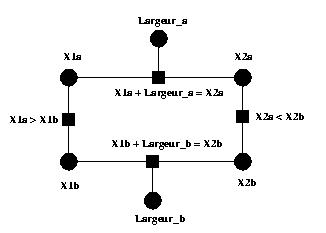
Figure V-18 : Cycle dans le graphe de contraintes
De manière à contourner ces limites, il est donc nécessaire d'effectuer un
prétraitement pour éliminer ces cycles quand cela est possible, ou de limiter
les déplacements permis à l'auteur, par exemple, en interdisant à un objet de
modifier son composite englobant. En effet, cela se traduit par la suppression
des relations père/fils dans le graphe de contraintes et le système de gestion
de contraintes restreindra les manipulations de l'auteur de manière à ne pas
déformer l'objet père (7.3.2). Par exemple, lorsque l'auteur modifie la
variable X2a, on peut supprimer la contrainte qui lie X2a et X2b pour casser
le cycle.
Le mécanisme de résolution propagera la déformation de X2a sur le graphe de
contraintes. Cependant, le mécanisme de résolution peut choisir de modifier la
largeur de B pour satisfaire l'ensemble de contraintes. Cette modification est
pertinente du fait qu'il n'y a plus la contrainte (X2a < X2b).
Il faudra donc orienter le résolveur (en ajoutant des poids sur les
contraintes) de telle manière qu'il satisfasse la contrainte que nous avons
enlevée pour supprimer le cycle.
Ce mécanisme de suppression des cycles qui doit être recalculé à chaque
opération d'édition (car il est dépendant de la variable affectée) est basé
sur le travail de Laurent Carcone [Carcone97] lors de l'expérimentation. Le
temps nécessaire pour résoudre ces cycles sera compté dans le temps de
résolution.
8.1.3 Résolveurs
ad hoc évalués
Comme nous avons pu le voir dans le chapitre précédent deux résolveurs ont été
développés de manière spécifique pour notre utilisation (HPC2, AVT). Nous
évaluerons leurs performances et leurs qualités par rapport aux autres
résolveurs.
On rappelle que l'algorithme de la vue temporelle nécessite la connaissance
des domaines de validité des variables, et de ce fait impose que le résolveur
de contraintes utilisé pendant les phases d'ajout / retrait d'objet ou de
relation maintienne ces informations.
De plus, nous avons défini un résolveur, le résolveur nul, il propage les
valeurs sans calculer de nouvelles valeurs ni s'assurer de la cohérence du
document. Cela nous permettra d'isoler le temps pris effectivement par le
résolveur du temps mis par le système pour prendre en compte la modification
et la propager.
8.1.4 Orientation des résolveurs de
contraintes
Pour tous les résolveurs de contraintes supportant la définition de
contraintes hiérarchiques nous avons utilisé le mécanisme suivant pour
orienter la rechercher. La définition des poids sur les contraintes, et
l'ajout de contraintes pour orienter la recherche nécessite un prétraitement
pour chaque opération d'édition.
Par exemple, pour orienter la résolution du graphe de contraintes de la
section 8.1.2 il faut :
- Rajouter une contrainte de poids de 5 qui indique que la variable
Largeur_a est constante ceci afin de favoriser la modification de X1a
par rapport à Largeur_a.
- Définir un poids de 3 sur la contrainte X1b + largeur_b = X2b et un
poids de 4 sur la contrainte X1a=X1b. Cela aura pour effet de favoriser
la modification de X2a par rapport à X2b.
- Rajouter une contrainte de poids de 5 qui indique que la variable
Largeur_b est constante ceci afin de favoriser la modification de X2b
par rapport à Largeur_b.
Notons qu'entre deux opérations d'édition, la politique d'orientation reste
globalement la même et ne nécessite que quelques modifications locales. Le
temps de prétraitement est comptabilisé dans le temps de résolution.
8.2 Expérimentation
Les tests ont été réalisés sur un Pentium II, 400 MHz .
8.2.1 Description des tests d'évaluation
Pendant cette phase d'évaluation, notre intérêt s'est porté sur trois points :
- Le temps mis pour calculer la nouvelle solution.
- La qualité de la nouvelle solution en fonction de la précédente.
- La capacité du résolveur à supporter le facteur d'échelle.
Pour réaliser ces tests on a généré deux groupes de documents, le premier
contenait 100 objets par document (Figure V-19) et le second 1000 objets
(Figure V-20).
Chaque session test est composée des étapes suivantes :
- Ouvrir le document et mesure du temps nécessaire au résolveur pour
calculer une solution initiale à partir du jeu de contraintes et de
l'ensemble des variables.
- Edition:
- Ajout ou retrait d'un objet.
- Ajout ou retrait d'une relation temporelle ou spatiale.
- Modification d'un attribut spatial ou temporel par manipulation
directe, c'est-à-dire que l'auteur déplace ou retaille l'objet à
l'écran dans la vue de présentation ou dans la vue temporelle.
Pour chacun des résolveurs nous avons utilisé une des deux méthodes
(heuristique ou contraintes pondérées) pour orienter la recherche de solution.
Le symbole L sera utilisé quand le résolveur
n'aura pas été capable de trouver une solution, ou qu'il aura généré une
erreur due, par exemple, à un problème de mémoire. Le symbole Non
signifie que le résolveur est incapable de traiter l'opération d'édition. Dans
la Figure V-21, nous présentons les résultats qualitatifs, le critère de
qualité a été calculé en mesurant la distance entre la solution générée par
Maple et celle du résolveur que l'on étudie. Les paramètres utilisés pour
cette fonction étaient : a = b = x = d = e = 0.2 (voir 5.3.1).
+,- : signifie ajout / retrait d'objet ou de relation ;
Dep. : signifie déplacement ;
Ret. : signifie retaillage.
| Résolveur |
Ouverture
|
Edition
|
|
Objets
|
Relations
|
Attributs
|
|
+
|
-
|
Spatiale
|
Temporelle
|
Spatial
|
Temporel
|
|
+
|
-
|
+
|
-
|
Dep.
|
Ret.
|
Dep.
|
Ret.
|
| Globaux |
Cassowary |
4.4s |
0.4s |
0.2s |
0.6s |
0.3s |
0.4s |
0.2s |
0.5s |
0.5s |
0.4s |
0.4s |
| JSolver |
4.5s |
0.5s |
4.5s |
1.2s |
4.5s |
1s |
4.5s |
4.5s |
4.5s |
4.5s |
4.5s |
| Maple |
18mn |
18mn |
18mn |
18mn |
18mn |
18mn |
18mn |
18mn |
18mn |
18mn |
18mn |
| Local |
Deltablue |
4.5s |
0.2s |
0.1s |
0.5s |
0.3s |
0.4s |
0.3s |
0.2s |
0.2s |
0.2s |
0.2s |
| Nul |
|
3s |
0.1s |
0.1s |
0.1s |
0.1s |
0.1s |
0.1s |
0.05s |
0.05s |
0.05s |
0.05s |
| Ad'hoc |
HPC2 |
20.2s |
0.15s |
0.15 |
Non |
Non |
1s |
20.2s |
Non |
Non |
12s |
12s |
| AVT |
Non |
Non |
Non |
Non |
Non |
Non |
Non |
Non |
Non |
0.1s |
0.1s |
Figure V-19 : Résultats quantitatifs pour 100 objets
| Résolveur |
Ouverture |
Edition
|
|
Objets
|
Relations
|
Attributs
|
|
+
|
-
|
Spatiale
|
Temporelle
|
Spatial
|
Temporel
|
|
+
|
-
|
+
|
-
|
Dep.
|
Ret.
|
Dep.
|
Ret.
|
|
Global
|
Cassowary |
192s
|
0.7s
|
0.2s
|
5s
|
0.3s
|
4s
|
0.2s
|
3.5s
|
3.5s
|
2.3s
|
2.3s
|
| Jsolver |
L
|
L
|
L
|
L
|
L
|
L
|
L
|
L
|
L
|
L
|
L
|
| Maple |
> 1h
|
> 1h
|
> 1h
|
> 1h
|
> 1h
|
> 1h
|
> 1h
|
> 1h
|
> 1h
|
> 1h
|
> 1h
|
| Local |
Deltablue |
11.4s
|
0.4s
|
0.2s
|
1s
|
0.3s
|
1s
|
0.3s
|
0.5s
|
0.5s
|
0.5s
|
0.5s
|
| Nul |
|
8s
|
0.1s
|
0.1s
|
0.1s
|
0.1s
|
0.1s
|
0.1s
|
0.05s
|
0.05s
|
0.05s
|
0.05s
|
| Ad'hoc |
HPC2 |
L
|
L
|
L
|
L
|
L
|
L
|
L
|
L
|
L
|
L
|
L
|
| AVT |
Non
|
Non
|
Non
|
Non
|
Non
|
Non
|
Non
|
Non
|
Non
|
0.1s
|
0.1s
|
Figure V-20 : Résultats quantitatifs pour 1000 objets
Dans la Figure V-21, nous présentons les résultats qualitatifs. On peut
noter qu'une valeur de qualité de 0 indique une solution parfaite en fonction
du critère défini, une valeur supérieure à 0.2 indique une solution non
satisfaisante.
| Résolveur |
ouverture
|
Edition
|
|
Objets
|
Relations
|
Attributs
|
|
+
|
-
|
Spatiale
|
Temporelle
|
Spatial
|
Temporel
|
|
+
|
-
|
+
|
-
|
Dep.
|
Ret.
|
Dep.
|
Ret.
|
| Globaux |
Cassowary |
0.1
|
0
|
0
|
0.1
|
0
|
0.1
|
0
|
0.05
|
0.05
|
0.05
|
0.05
|
| jSolver |
0.1
|
0
|
0
|
0.05
|
L
|
0.05
|
L
|
0
|
0
|
0
|
0
|
| Maple |
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| Local |
Deltablue |
0.3
|
0
|
0
|
0.3
|
0
|
0.3
|
0
|
0.4
|
0.4
|
0.4
|
0.4
|
| Od'hoc |
HPC2 |
0.1
|
0
|
0
|
Non
|
Non
|
0
|
0
|
Non
|
Non
|
0
|
0
|
| AVT |
Non
|
Non
|
Non
|
Non
|
Non
|
Non
|
Non
|
Non
|
Non
|
0.05
|
0.05
|
Figure V-21 : Résultats qualitatifs pour 1000 objets
8.2.2 Analyse des résultats de
l'évaluation
Les résultats quantitatifs et qualitatifs montrent que les performances
dépendent de l'opération d'édition réalisée. En effet, les opérations révèlent
les capacités intrinsèques des résolveurs. Par exemple, de bonnes performances
temporelles sont obtenues avec HPC2, lors de l'ajout de relations, du fait
qu'il est capable de maintenir les domaines minimaux sur les intervalles, mais
il a de très mauvaises performances temporelles lors du retrait de relations.
Cela est dû au fait qu'il doit reconsidérer à nouveau l'ensemble des
contraintes, car cet algorithme n'est pas adapté au relâchement des
intervalles minimaux. On remarque que jSolver a le même comportement.
Le meilleur résolveur en terme de temps de réponse est Deltablue, cependant
les limites que nous avons décrites dans la section précédente sont trop
contraignantes dans un contexte d'édition, ce qui se remarque dans les
résultats qualitatifs. Le résolveur qui offre donc le meilleur compromis entre
les critères de performance et de qualité est Cassowary.
Les résultats montrent également la différence de sensibilité des
résolveurs face au facteur d'échelle :
- HPC2 atteint vite ses limites lorsque le nombre d'objets manipulés
devient important. Cette limite est liée à la manipulation d'un graphe
complet par l'algorithme.
- jSolver atteint aussi rapidement ses limites du fait de la taille des
domaines manipulés.
L'algorithme AVT nécessite les domaines minimaux pour être capable de calculer
une nouvelle solution. Ce calcul est complexe et coûteux en temps. Cet
algorithme ne peut donc pas être utilisé lors de l'ajout ou du retrait d'objet
ou de relation. Cependant, cet algorithme est très puissant pour calculer le
déplacement et le retaillage d'objets (avec les restrictions décrites dans le
chapitre précédant). Il est donc particulièrement adapté aux manipulations de
navigation dans la vue temporelle et d'exécution.
Un point important à souligner est que les résolveurs les plus performants
sont ceux qui ont les plus mauvaises performances qualitatives, car n'offrant
pas de mécanismes efficaces de contrôle pour orienter la recherche de
solution.
8.3 Proposition d'un algorithme
polymorphe
Les résultats précédents montrent que le meilleur algorithme dépend de
l'opération d'édition. De cette analyse, nous avons décidé de combiner
plusieurs résolveurs de contraintes de manière à utiliser le plus adapté pour
chacune des opérations d'édition.
L'idée de combiner plusieurs résolveurs de contraintes a déjà été
expérimentée dans différents contextes. On peut citer les résolveurs SkyBlue
[Sannella95], Ultraviolet [Borning98] et DETAIL [Hosobe96]. Lors de la
combinaison de différents résolveurs se posent plusieurs problèmes, on peut
citer :
- Le partage ou la synchronisation des différentes structures de données
;
- Les critères de chargement des résolveurs ;
- Le pilotage des résolveurs. Le pilotage peut être externe dans ce
cas c'est un module qui gère la coopération entre les résolveurs, ou
hiérarchique et dans ce cas c'est un des résolveur qui contrôle les
autres résolveurs.
Les résolveurs Skyblue et Ultraviolet fonctionnent sur le même mécanisme. Un
résolveur principal, qui travaille sur le graphe de contraintes résout tant
qu'il le peut le graphe de contraintes. Lorsqu'il trouve une sous-partie du
graphe, avec une topologie telle qu'il ne peut la traiter (ou la traiter de
manière efficace), il fait appel à un résolveur secondaire pour traiter cette
partie de graphe. Les résolveurs secondaires sont en général moins performants
que les résolveurs primaires, mais ils permettent d'étendre leur expressivité.
Dans notre contexte, la topologie de nos graphes de contraintes est telle, que
ces résolveurs feraient constamment appel aux résolveurs secondaires, et
perdraient ainsi tous les avantages du résolveur primaire.
Le résolveur DETAIL est un résolveur multicouches, c'est à dire qu'il est
composé d'un résolveur principal et de sous-résolveurs. Le résolveur principal
produit le graphe de contraintes et applique dessus une propagation locale. Au
cours de cette propagation il divise le graphe en cellules correspondant à des
zones du graphe facilement calculables. Chacune de ces cellules sera donnée à
un sous-résolveur qui calculera une valuation pour chacune des variables de la
cellule. Le résolveur choisira un sous-résolveur optimisé pour la topologie et
les contraintes de la cellule. DETAIL ne traite pas les inégalités et obtient
des performances temporelles proches de Deltablue.
L'algorithme polymorphe que nous avons utilisé est une combinaison de
Deltablue et de Cassowary. La coopération entre ces deux algorithmes ne se
fait pas pour la résolution d'un problème, mais une entité de pilotage et de
contrôle externe aux résolveurs choisit, en fonction du problème, quel
résolveur elle utilisera. Nous utilisons par exemple Deltablue lors de
l'ouverture du document ainsi que pour l'ajout d'objet. Nous utilisons
Cassowary pour toutes les autres opérations d'édition du fait qu'il est moins
restrictif que Deltablue. L'utilisation de Deltablue, lors de l'étape
d'ouverture n'est pas trop restrictive, en effet, à cette étape, il n'est pas
important de manipuler toutes les contraintes, on peut retirer celles qui
introduisent des informations redondantes ([Carcone97]).
La principale difficulté de cette coopération sera la synchronisation des
différentes structures de données (celle de Kaomi, celle de Deltablue et celle
de Cassowary). Cette synchronisation se fait grâce à la structure de données
de Kaomi. Avant de résoudre un problème, le résolveur vérifie que ses données
sont cohérentes par rapport à celles de Kaomi, et à la fin de la résolution,
le résolveur met les structures de données de Kaomi à jour.
Dans la Table 4, on peut voir que l'algorithme polymorphe n'est pas celui
qui obtient les meilleurs performances temporelles, cela est lié au fait que
le temps nécessaire pour prendre en compte une opération d'édition est
composée de deux parties : le temps pour construire les informations du
résolveur et le temps nécessaire pour calculer la nouvelle solution. Si nous
utilisons les deux algorithmes, il faut aussi compter un temps pour mettre à
jour les informations du résolveur qui n'est pas utilisé.
Malgré cela, ce résolveur semble très prometteur et c'est lui qui offre
globalement le meilleur rapport temps/qualité.
| Ouv. |
Editon |
|
Objets
|
Relation
|
Attributs
|
|
+
|
-
|
Spatial
|
Temporel
|
Spatial
|
Temporel
|
| + |
- |
+ |
- |
Dep. |
Ret. |
Dep. |
Ret. |
| 100 objets / document |
5.5s |
0.3s |
0.2s |
0.7s |
0.4s |
0.5s |
0.3s |
0.5s |
0.4s |
0.4s |
| 1000 objets / document |
13.2s |
0.6s |
0.3s |
2s |
0.4s |
1.7s |
0.4s |
0.7s |
2.4s |
2.5s |
Figure V-22 : Résultats de l'algorithme polymorphe
9. Apports et limites des contraintes pour l'édition
directe
Dans Kaomi, nous utilisons actuellement une implémentation de l'algorithme
polymorphe.
L'utilisation des technologies contraintes a permis de faciliter la tâche
de conception de la boîte à outils et, comme nous le verrons par la suite, de
faciliter la tâche de l'auteur dans les différents environnements auteur
construits à l'aide de la boîte à outils.
Dans la réalisation des services de Kaomi, les contraintes ont permis de
:
- Faciliter la tâche de conception et les possibilités d'extension en
généralisant la spécification des contraintes à résoudre.
- Mettre en commun les mécanismes de vérification de formatage pour les
différents formats de fichiers.
- Rendre l'extension des relations accessibles par l'auteur sans pour
autant remettre en cause les mécanismes de résolution.
- Permettre la mise en place d'une politique d'orientation générale pour
le formatage ainsi que la possibilité de la modifier facilement.
D'un point de vue édition, les contraintes ont permis de :
- Réaliser une édition incrémentale avec un formatage dynamique lors des
opérations d'édition.
- Réaliser une édition par manipulation directe dans la vue temporelle
et spatiale, avec maintien des relations et vérification de la cohérence
en cours de manipulation.
- Faciliter l'expression du scénario spatial et temporel grâce au
formalisme à base de contraintes offert par Kaomi.
Cependant, malgré ces apports, l'utilisation des contraintes présente encore
des limites :
- Le choix du résolveur influe sur la capacité du système à assurer la
cohérence du document. En effet, l'utilisation d'un algorithme de
résolution non complet, de type Deltablue nous oblige à réaliser une
phase de vérification de la cohérence explicite.
- Les performances temporelles des résolveurs sont inversement
proportionnelles au nombre d'objets manipulés. Ces techniques sont
encore difficilement utilisables pour de gros documents (présentation
contenant 10000 objets).
- Traitement des objets imprédictifs, en effet l'intégration d'objets
imprédictifs dans les relations d'égalité et d'implication, pose de
nouveaux problèmes du fait que l'on ne peut pas formater statiquement le
document. Une méthode consiste à définir une fin prévue et une fin
effective sur chacun des objets. La difficulté est que le système ne
peut et ne doit pas affecter de valeur à ces variables du fait que leurs
valeurs ne seront connues que lors de l'exécution. La fin prévue
correspond à une durée calculée statiquement, et la fin effective
correspond à celle qui aura lieu dynamiquement. Dans le cas d'objets
contrôlables interrompus par un objet incontrôlable, ces deux valeurs de
fin sont différentes. Statiquement, il faut assurer qu'il existe au
moins une solution. De plus il faut vérifier que toutes les exécutions
seront cohérentes ce qui devient une tâche complexe et non réalisable en
temps polynomial [Mackworth85].














